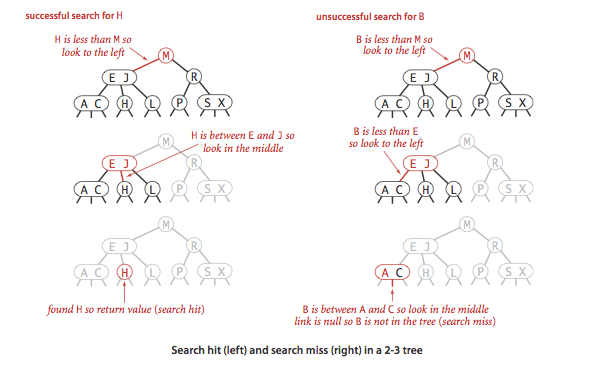
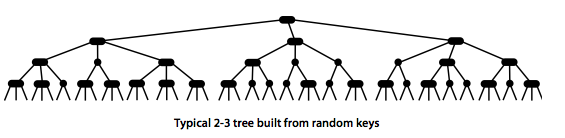
2-3 Trees

TL;DR

A 2-3 tree is a type of balanced search tree data structure that allows for efficient insertion, deletion, and search operations. It is similar to a binary search tree, but each node in a 2-3 tree can have up to two or three children, depending on the number of keys stored in the node.

In a 2-3 tree, each node can contain either one or two keys, and is always either a 2-node or a 3-node. A 2-node has one key and two children, while a 3-node has two keys and three children. The keys in a node are stored in sorted order, with the smallest key at the leftmost position and the largest key at the rightmost position.

The 2-3 tree has the property that all the leaves of the tree are at the same level, which makes it a balanced tree. This ensures that the height of the tree is logarithmic in the number of elements stored in the tree, leading to efficient search, insertion, and deletion operations.

Overall, 2-3 trees are an important data structure in computer science, and are commonly used in database systems and other applications where efficient search and insertion are important.

Additional Resources

• 2-3 Trees (Insertion, Deletion, Techniques) REUPLOAD | EducationAboutStuff : 19:17

Define

Purpose

2-3 trees are a type of self-balancing tree data structure that can be used to implement a variety of algorithms and data structures. They are similar to binary search trees, but have the advantage of better balancing, which ensures that the height of the tree remains small and operations such as insertions, deletions, and searches are efficient.

Here are some reasons why 2-3 trees can be useful:

Self-balancing

• Unlike ordinary binary search trees, 2-3 trees are designed to be self-balancing. This means that they automatically adjust their structure as data is added or removed, to ensure that the tree remains balanced and efficient.

Better worst-case performance

• 2-3 trees guarantee worst-case performance of \(O(log\ n)\) for most operations, including insertions, deletions, and searches. This makes them useful in applications where worst-case performance is important.

Efficient range queries

• Because 2-3 trees are balanced, they can efficiently perform range queries (i.e., finding all values within a given range). This can be useful in a variety of applications, such as database indexing.

Space-efficient

• 2-3 trees are relatively space-efficient compared to other balanced tree structures. This is because each node in a 2-3 tree can contain multiple keys and pointers, allowing more data to be stored in each node.

Overall, 2-3 trees are a versatile and efficient data structure that can be used in a variety of applications where balanced trees are needed.

Uses

Here are some examples of programs that would benefit from using 2-3 trees:

Databases

• 2-3 trees are commonly used in database indexing, where they can efficiently store and search large amounts of data. For example, a database that needs to perform range queries or support ordered traversal of data can use 2-3 trees to improve performance.

File systems

• 2-3 trees can also be used in file systems to efficiently store and search large numbers of files. For example, a file system that needs to perform frequent searches or lookups can use a 2-3 tree to reduce the time required to find specific files.

Network routing

• 2-3 trees can be used in network routing algorithms to efficiently route data packets between nodes in a network. For example, a routing algorithm that needs to find the shortest path between two nodes can use a 2-3 tree to quickly search for the best route.

Compiler symbol tables

• 2-3 trees can be used in compilers to efficiently store and search symbol tables, which are used to keep track of variables and functions in a program. For example, a compiler that needs to quickly find the definition of a variable or function can use a 2-3 tree to improve performance.

Spell checkers

• 2-3 trees can be used in spell checkers to efficiently store and search large dictionaries of words. For example, a spell checker that needs to quickly determine whether a given word is in its dictionary can use a 2-3 tree to reduce the time required for lookups.

Memory management

• Some memory management systems use 2-3 trees to keep track of allocated and free memory blocks, ensuring efficient allocation and de-allocation.

Overall, 2-3 trees can be used in any program that needs to efficiently store and search large amounts of data, and where balanced trees are needed to ensure good worst-case performance.

Components

2-node

has one data element and if it is an internal node, then it has two child nodes.

3-node

has two data elements and if this is an internal node, it has three child nodes.

4-node

has three data elements and if it is an internal node, it has four child nodes.

Symmetric order

• Inorder traversal yields keys in ascending order

Perfect Balance

• Every path from the root null link has same length

Operations

search

Compare search key against key(s) in node

Find Interval containing search key

Follow associated link (recursively)

search for \(H\) & \(B\)

Try it…

insert

Case 1

Insert in a node with only one data element

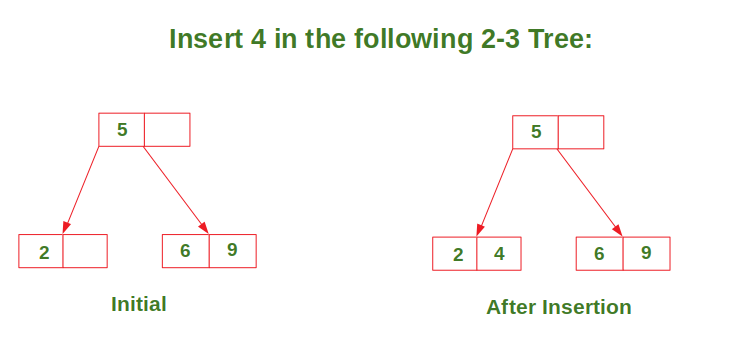
Try it…

Case 2

Insert in a node with two data elements whose parent contains only one data element

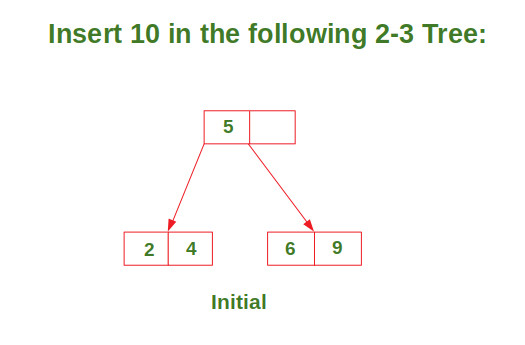
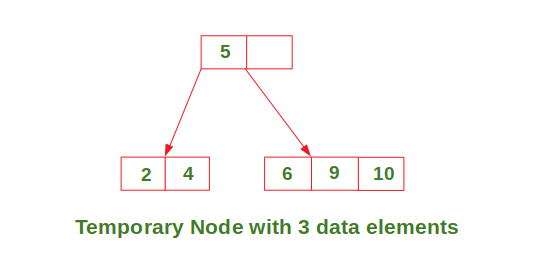
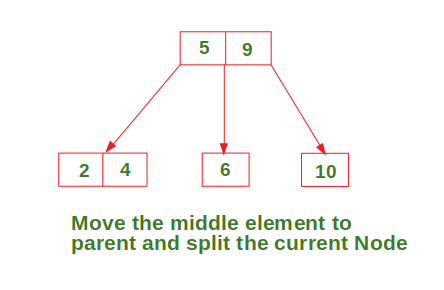
Try it…

Case 3

Insert in a node with two data elements whose parent also contains two data elements

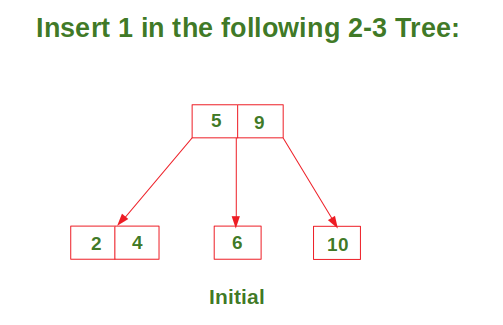
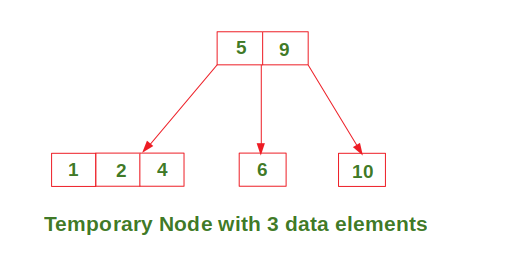
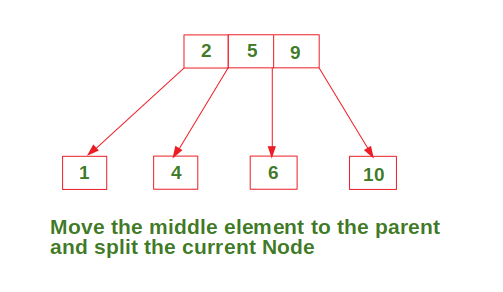
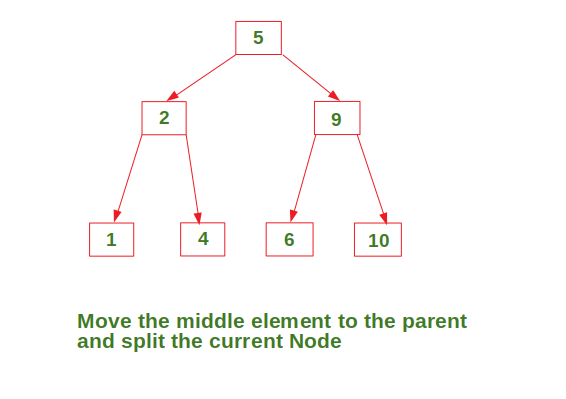
Try it…

All

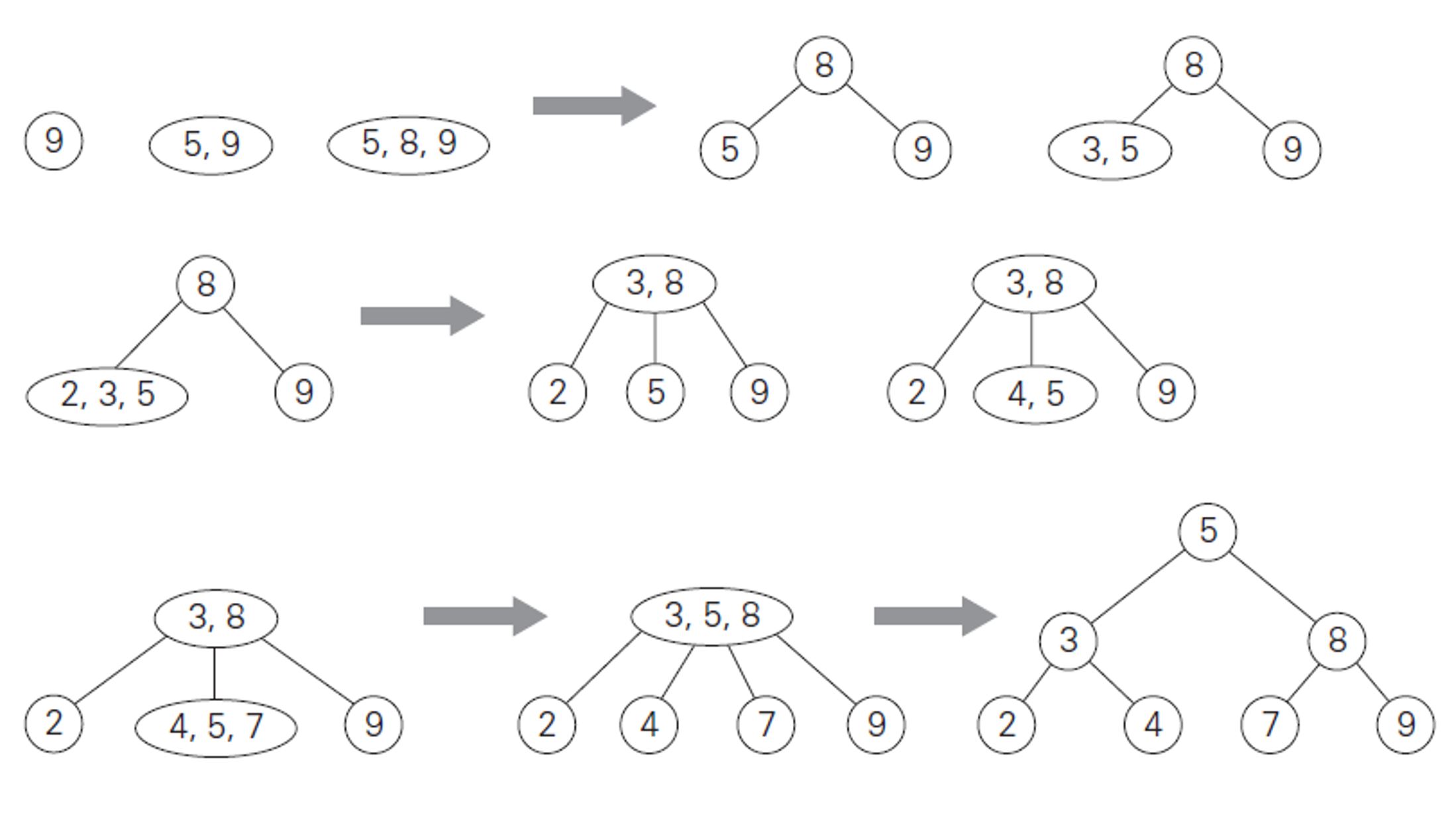
Fig. 28 \(tree\ = \{9, 5, 8, 3, 2, 4, 7 \}\)

delete

Considerations for deletion

• To delete a value, it is replaced by its in-order successor and then removed.

• If a node is left with less than one data value then two nodes must be merged together.

• If a node becomes empty after deleting a value, it is then merged with another node.

Starting Tree

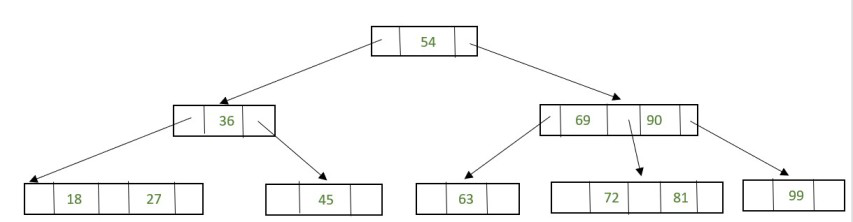
Objective: delete the following values from it… 69, 72, 99, 81

69

Swap it with its in-order successor, that is, 72. 69 now comes in the leaf node. Remove the value 69 from the leaf node.

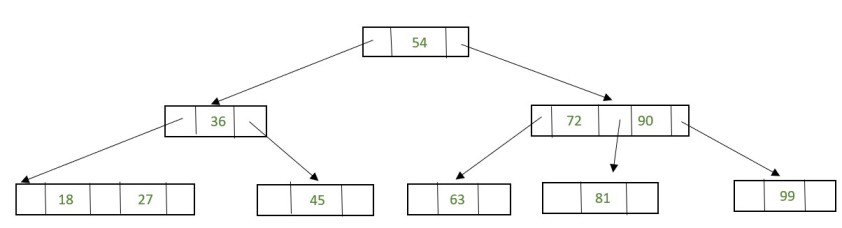
Fig. 29 After deletion 69

72

72 is an internal node.

To delete this value swap 72 with its in-order successor 81 so that 72 now becomes a leaf node. Remove the value 72 from the leaf node.

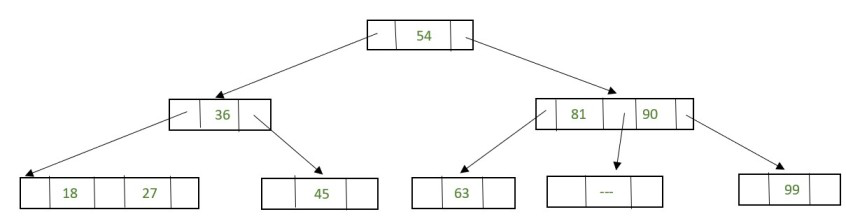
Fig. 30 After deletion 72

Now there is a leaf node that has less than 1 data value thereby violating the property of a 2-3 tree. So the node must be merged.

To merge the node, pull down the lowest data value in the parent’s node and merge it with its left sibling.

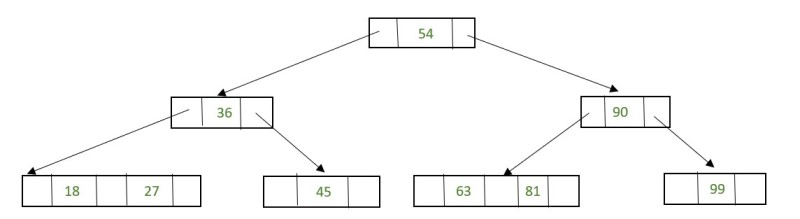
Fig. 31 Rebalancing to Satisfy 2-3 Tree property

99

99 is present in a leaf node, so the data value can be easily removed.

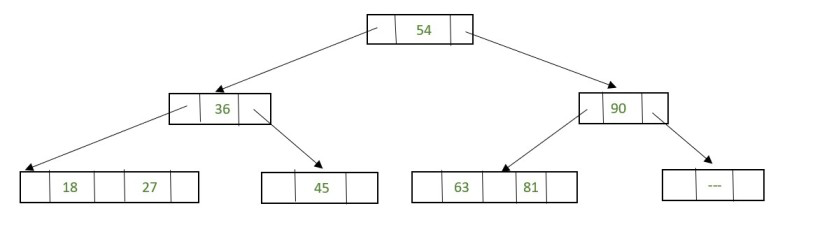
Fig. 32 After deletion 99

Now there is a leaf node that has less than 1 data value, thereby violating the property of a 2-3 tree.

So the node must be merged. To merge the node, pull down the lowest data value in the parent’s node and merge it with its left sibling.

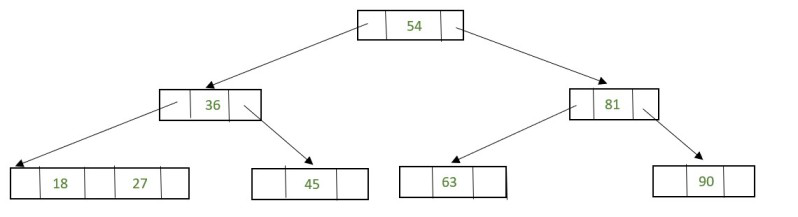
Fig. 33 Rebalancing to Satisfy 2-3 Tree Property

81

81 is an internal node

To delete this value swap 81 with its in-order successor 90 so that 81 now becomes a leaf node. Remove the value 81 from the leaf node.

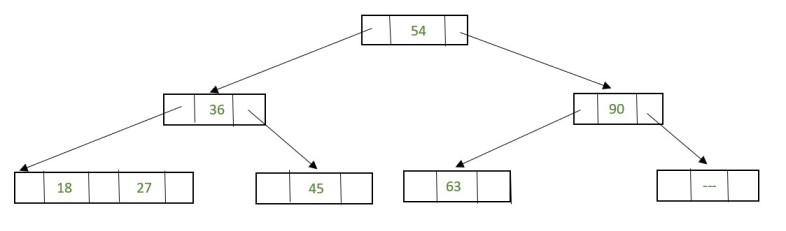
Fig. 34 After deletion 81

Now there is a leaf node that has less than 1 data value, thereby violating the property of a 2-3 tree. So the node must be merged.

To merge the node, pull down the lowest data value in the parent’s node and merge it with its left sibling.

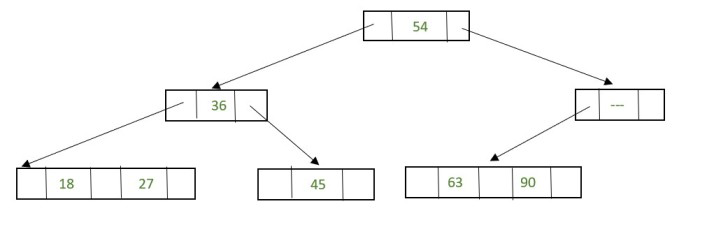
Fig. 35 Rebalancing to Satisfy 2-3 Tree property

As internal node cannot be empty. So now pull down the lowest data value from the parent’s node and merge the empty node with its left sibling

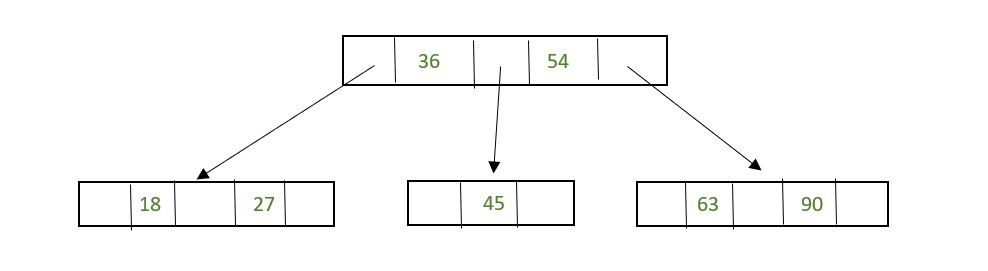
Fig. 36 Rebalancing to Satisfy 2-3 Tree property

NOTE: In a 2-3 tree, each interior node has either two or three children. This means that a 2-3 tree is not a binary tree.

Visual

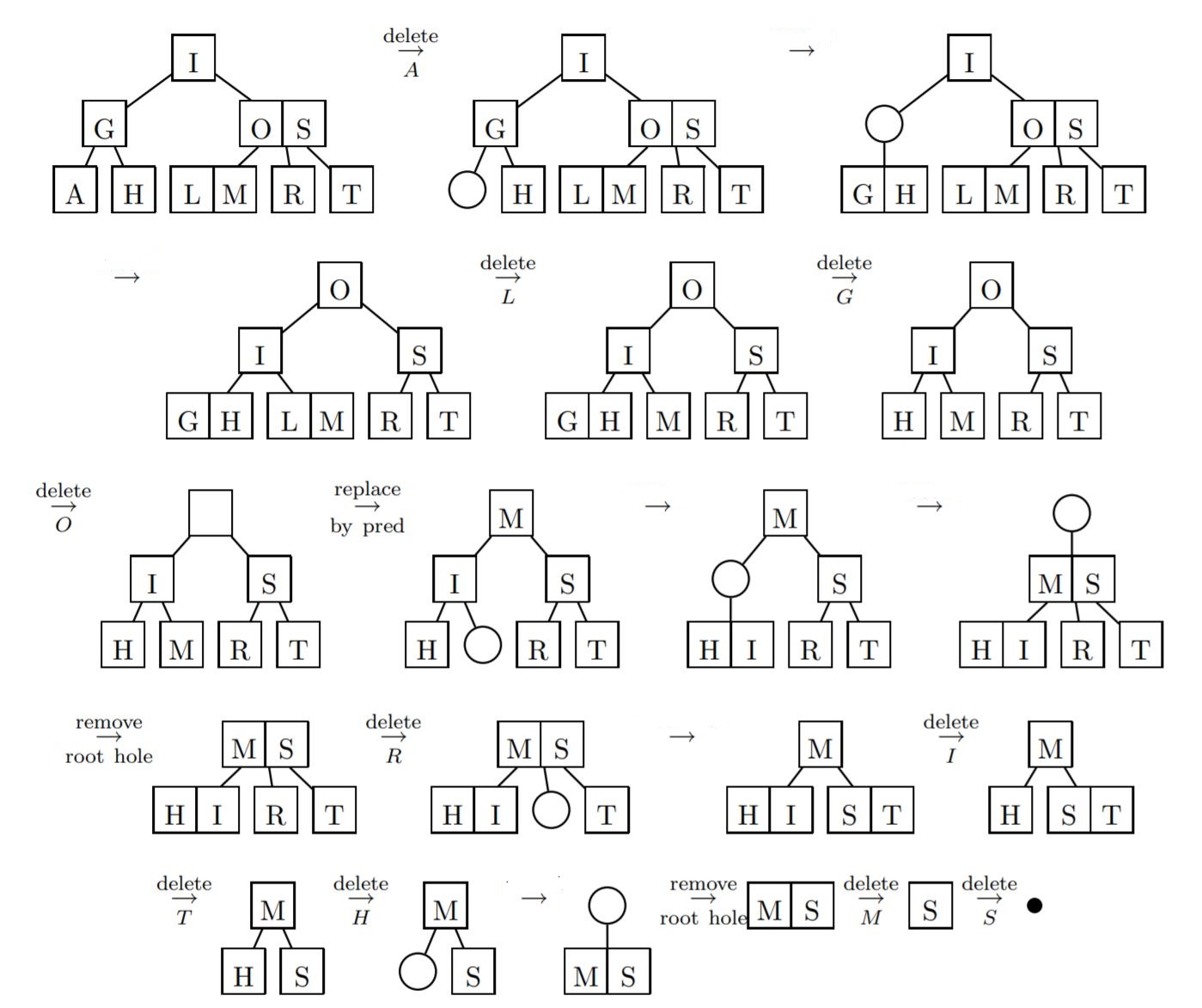
Fig. 37 Broad overview of deletions at different places

Consider

The three sets are identical minus their order… does it matter? Try them and see…

\(tree1 = \{13, 5, 18, 16, 19, 24, 1, 10, 3, 8, 12 \}\)
\(tree2 = \{24, 19, 12, 16, 5, 13, 1, 10, 8, 3, 18 \}\)
\(tree3 = \{19, 10, 18, 12, 13, 24, 1, 5, 3, 8, 16 \}\)

Try it…

Performance

Perfect balance

Every path from the root to null has the same length

Tree Height

• Min: \(log_3 \ n \approx 0.631\ \ log_2 \ n\)

• Max: \(log_2 \ n\)

• Between 12 and 20 for a million nodes

• Between 18 and 30 for a billion nodes

Bottomline

Guaranteed logarithmic performance for search and insert

Complexity

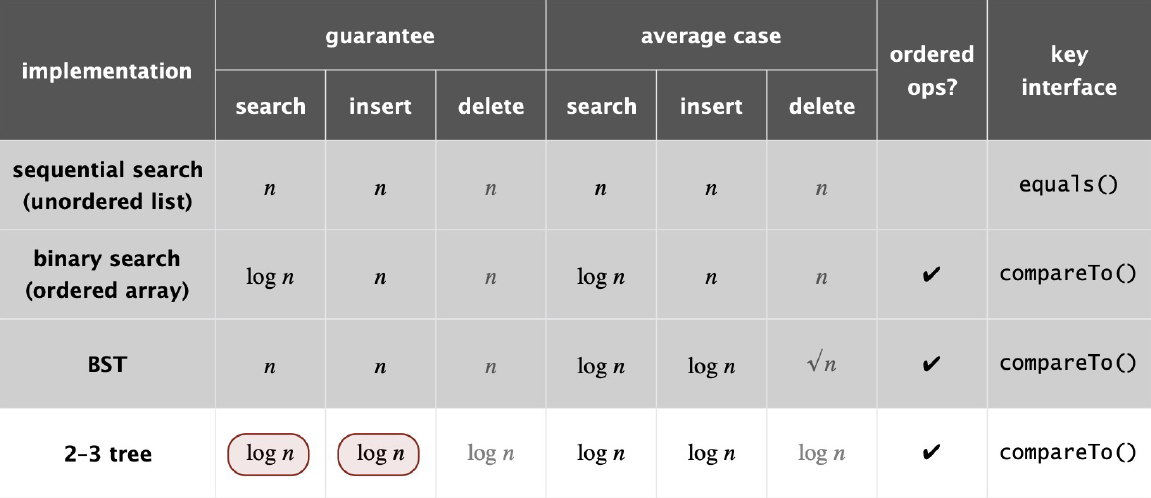
Fig. 38 but hidden constant \(c\) is large (depends on implementation)

Implementation

Direct implementation is complicated, because

• Maintaining multiple node types is cumbersome

• Need multiple compares to move down tree

• Need to move back up the tree to split 4-nodes

• Large number of cases for splitting

void put(Key key, Value val) {
  Node x = root;
  while (x.getCorrectChild(key) != null) {
    x = x.getCorrectChildKey();
    if (x.is4Node()) x.split();
  }
  if (x.is2Node()) x.make3Node(key, val) 
  else if (x.is3Node()) x.make4Node(key, val) 
}

Bottomline

Could do it, but there’s a better way