Dynamic Arrays#
Dynamic arrays are a common data structure used in computer programming to store a collection of elements of the same type. Unlike static arrays, which have a fixed size that cannot be changed at runtime, dynamic arrays can grow or shrink as needed.
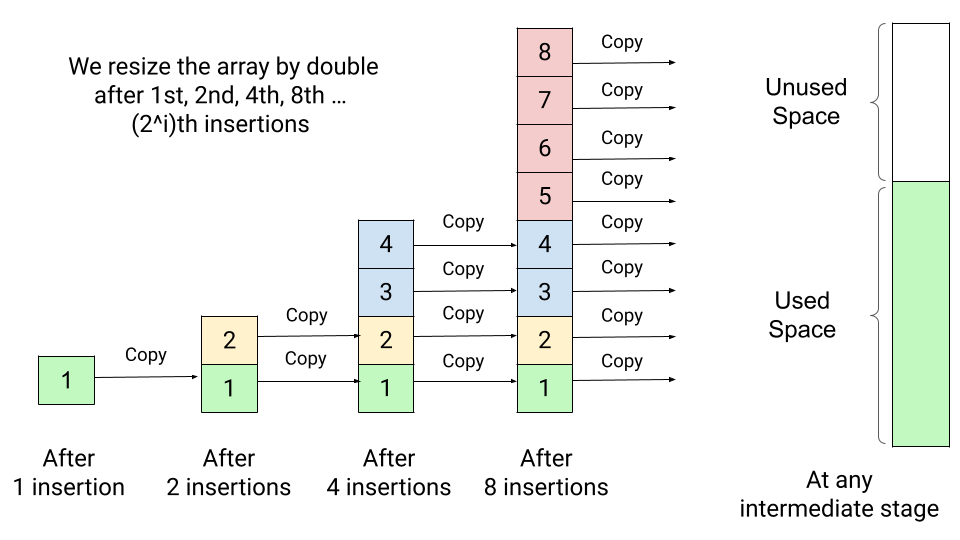
In a dynamic array, the elements are stored in contiguous memory locations, just like in a static array. However, a dynamic array has additional memory allocated beyond its initial size to allow for growth. When the dynamic array is full, it can be resized by allocating a new block of memory with a larger size and copying the existing elements into the new block. This process is called resizing.
Dynamic arrays are widely used because they provide a balance between the fast random access provided by static arrays and the flexibility of linked lists. They are particularly useful when the size of the collection is unknown or unpredictable at compile time. Dynamic arrays are commonly used in many algorithms, such as sorting and searching, where efficient random access to elements is important.
However, resizing a dynamic array can be an expensive operation, particularly when the array is large and the resizing occurs frequently. Therefore, careful consideration of the size of the dynamic array and the frequency of resizing is necessary when designing programs that use dynamic arrays.
Interfaces & Data Structures#
Interface
In programming, an interface is a blueprint or contract that defines a set of methods or behaviors that a class must implement.
An interface specifies the method signatures (function declarations) and sometimes constants or properties that a class implementing the interface should provide.
Interfaces enable polymorphism and provide a way to define common behavior that multiple classes can adhere to.
In many programming languages, including Java and C#, interfaces are used to achieve abstraction and enforce a certain level of consistency and structure across related classes.
Data Structure
In programming, a data structure is a way of organizing and storing data to enable efficient manipulation and access.
Data structures define how data is organized, stored, and accessed in computer memory.
Different data structures are designed to handle specific types of data and perform operations such as insertion, deletion, searching, and sorting.
Common examples of data structures include arrays, linked lists, stacks, queues, trees, graphs, and hash tables.
Code sample
public interface Shape {
double getArea();
double getPerimeter();
}
public class Circle implements Shape {
private double radius;
public Circle(double radius) {
this.radius = radius;
}
public double getArea() {
return Math.PI * radius * radius;
}
public double getPerimeter() {
return 2 * Math.PI * radius;
}
}
public class Rectangle implements Shape {
private double length;
private double width;
public Rectangle(double length, double width) {
this.length = length;
this.width = width;
}
public double getArea() {
return length * width;
}
public double getPerimeter() {
return 2 * (length + width);
}
}
Code sample
#include <iostream>
#include <vector>
int main() {
std::vector<int> numbers; // Declare a dynamic array (vector)
numbers.push_back(10); // Add element 10 at the end of the vector
numbers.push_back(20); // Add element 20 at the end of the vector
for (int number : numbers) {
std::cout << number << " "; // Output: 10 20
}
return 0;
}
Arrays#
An array is a contiguous sequence of elements of the same type
Each element can be accessed using index
//array declaration by specifying size
int myarray1[100];
//can also declare an array of user specified
//size (must be const for many compilers!)
int n = 8;
int myarray2[n];
// can declare and initialize elements
double arr[] = { 10.0, 20.0, 30.0, 40.0 };
// size is implicitly understood by the compiler when initialized at declaration
// alternative way
int arr[5] = { 1, 2, 3 };
// size is explicitly manipulated for the compiler
// size = 5, element count = 3, empty elements remaining = 2
Static arrays#
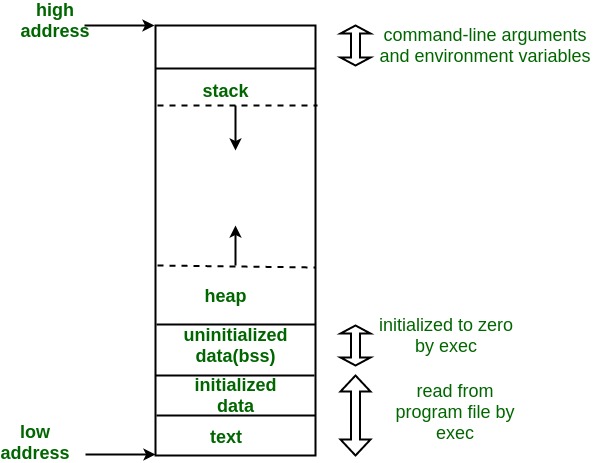
So far… we have seen examples of arrays, allocated in the stack (fixed length)
//array declaration by specifying size
int myarray1[100];
You can allocate memory dynamically, allocated in the heap (still fixed length)
int *myarray = new int[100];
//...
//work with the array
//...
delete []myarray;
Memory Allocation#
Stack
It’s a temporary memory allocation scheme where the data members are accessible only if the method( ) that contained them is currently running.
It allocates or de-allocates the memory automatically as soon as the corresponding method completes its execution.
Stack memory allocation is considered safer as compared to heap memory allocation because the data stored can only be accessed by the owner thread.
Memory allocation and de-allocation are faster as compared to Heap-memory allocation.
Stack memory has less storage space as compared to Heap-memory.
Heap (memory, not structure)
This memory allocation scheme is different from the Stack-space allocation, here no automatic de-allocation feature is provided. We need to use a Garbage collector to remove the old unused objects in order to use the memory efficiently.
The processing time(Accessing time) of this memory is quite slow as compared to Stack-memory.
Heap memory is also not as threaded-safe as Stack-memory because data stored in Heap-memory are visible to all threads.
The size of the Heap-memory is quite larger as compared to the Stack-memory.
Comparison Chart
Parameter |
STACK |
HEAP |
|---|---|---|
Basic |
Memory is allocated in a contiguous block. |
Memory is allocated in any random order. |
Allocation and De-allocation |
Automatic by compiler instructions. |
Manual by the programmer. |
Cost |
Less |
More |
Implementation |
Easy |
Hard |
Access time |
Faster |
Slower |
Main Issue |
Shortage of memory |
Memory fragmentation |
Locality of reference |
Excellent |
Adequate |
Safety |
Thread safe, data stored can only be accessed by the owner |
Not Thread safe, data stored visible to all threads |
Flexibility |
Fixed-size |
Resizing is possible |
Data type structure |
Linear |
Hierarchical |
Preferred |
Static memory allocation is preferred in an array. |
Heap memory allocation is preferred in the linked list. |
Size |
Small than heap memory. |
Larger than stack memory. |
Memory allocation is an essential aspect of data structures and algorithms as it determines how memory is allocated and used to store data. Data structures are designed to efficiently organize and store data in memory, and algorithms use these data structures to perform operations on the data.
In general, there are two types of memory allocation: static and dynamic. Static memory allocation refers to memory allocation that is fixed at compile-time and cannot be changed at runtime. This is typically used for variables that have a fixed size and do not need to be resized during program execution.
Dynamic memory allocation, on the other hand, refers to memory allocation that is done at runtime and can be resized as needed. This is typically used for data structures that need to grow or shrink in size as data is added or removed.
One common data structure that uses dynamic memory allocation is the linked list. In a linked list, each element in the list is stored in a node that contains a pointer to the next node in the list. The nodes can be dynamically allocated as needed, allowing the list to grow or shrink as data is added or removed.
Another common data structure that uses dynamic memory allocation is the dynamic array. In a dynamic array, the size of the array can be dynamically resized as needed, allowing for efficient memory usage.
Memory allocation is an important consideration when designing and implementing data structures and algorithms. Efficient memory usage can greatly improve the performance of an algorithm, while inefficient memory usage can lead to performance problems or even crashes. Therefore, it is important to carefully consider the memory requirements of a data structure or algorithm and optimize memory usage wherever possible.
What if…?
Case 1
We don’t know the max size of an array before running the program!
user specified inputs/decisions!
e.g. read an image or video and display
Case 2
The sequence changes over time (during the execution of the program)
e.g. you develop a text editor and represent the sequence of characters as an array
Question
Which data structure (studied so far) would you use in each case?
Dynamic Arrays#
Dynamically allocated arrays that change their size over time
can grow automatically
can shrink automatically
Operations on arrays
appendremove_lastget\(\Theta(1)\)set\(\Theta(1)\)
First try#
Start with an empty array
For every append:
increase the size of the array by 1 then write the new element
For every remove_last:
remove the last element and then decrease the size of the array by 1
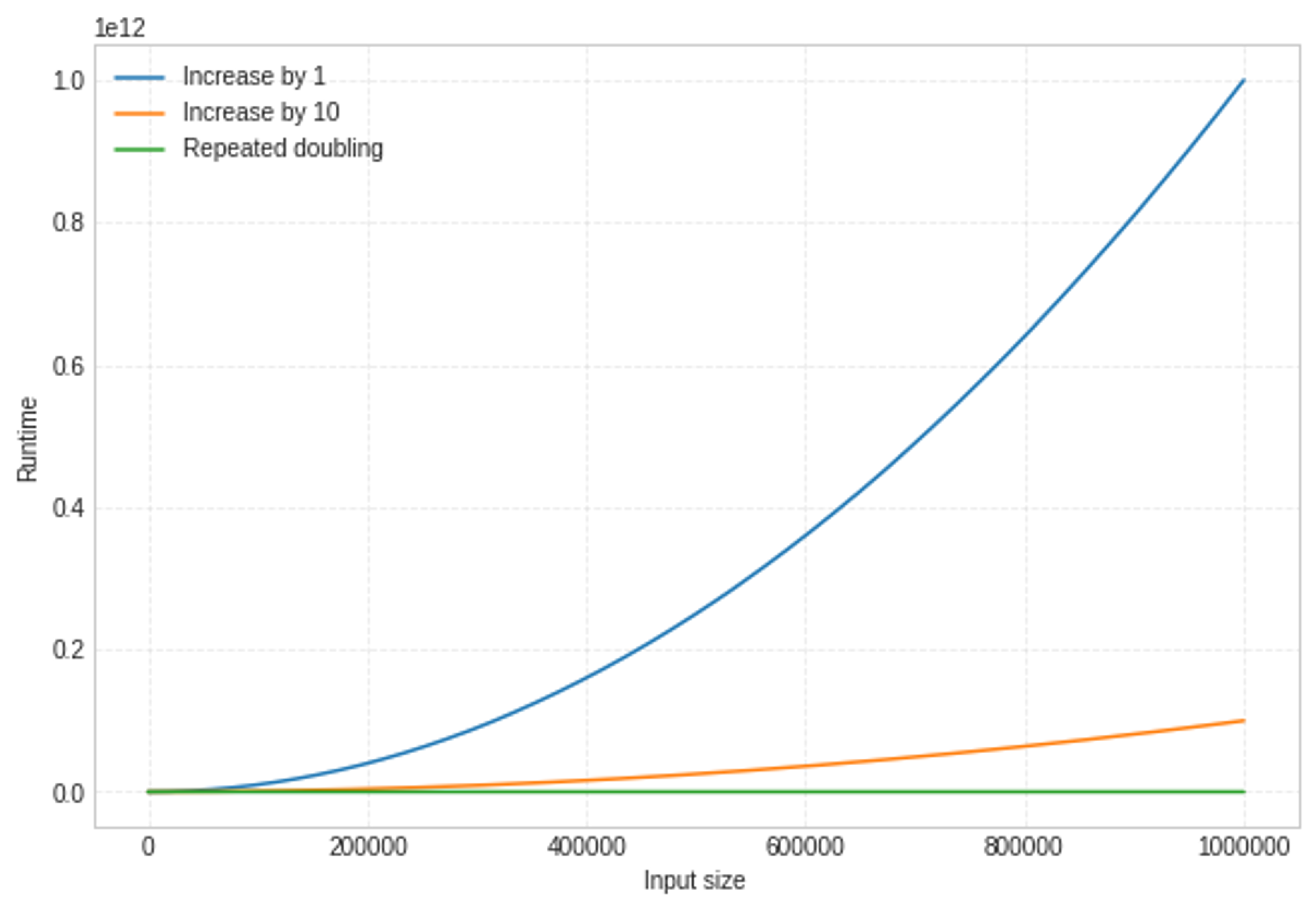
Analyzing cost#
Count array accesses (reads and writes) of adding first \(n\) elements
will ignore the cost of allocating/de-allocating arrays
\(n\) |
\(append\) |
\(copy\) |
|---|---|---|
Each row indicates the number of reads and writes necessary for appending an element into an existing array of length \(n\)
Note: think arithmetic sequences and arithmetic series
Count array accesses (reads and writes) of adding first \(n = 2^i\) elements
will ignore the cost of allocating/de-allocating arrays
Each row indicates the number of reads and writes necessary for appending an element into an existing array of length \(n\)
Note: think geometric sequences and geometric series