Binary Search Trees#
Binary Tree#
Overview
A binary tree is a hierarchical data structure consisting of nodes.
Each node contains a value and references to its left and right children.
The left child is smaller than the parent, while the right child is larger.
Implementing binary trees#
- Node
\(data\)
\(left\) child
\(right\) child
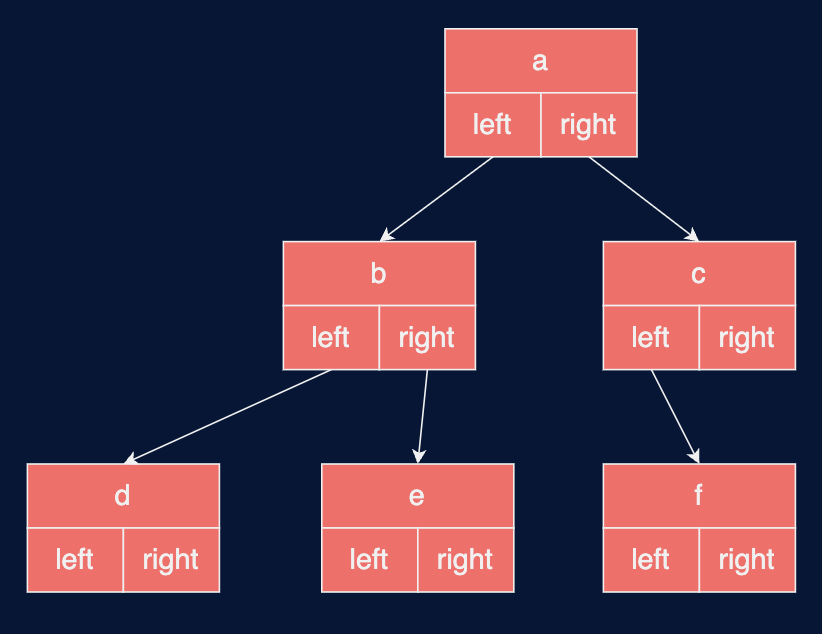
\(tree = \{a, b, c, d, e, f\}\)
\(k\)-ary trees#
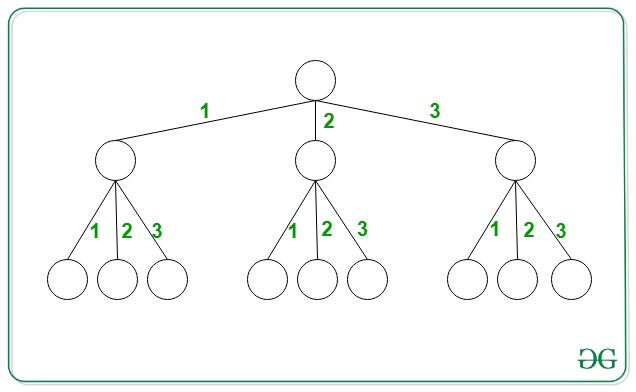
Fig. 14 Every node has between \(0\) and \(k\) children#
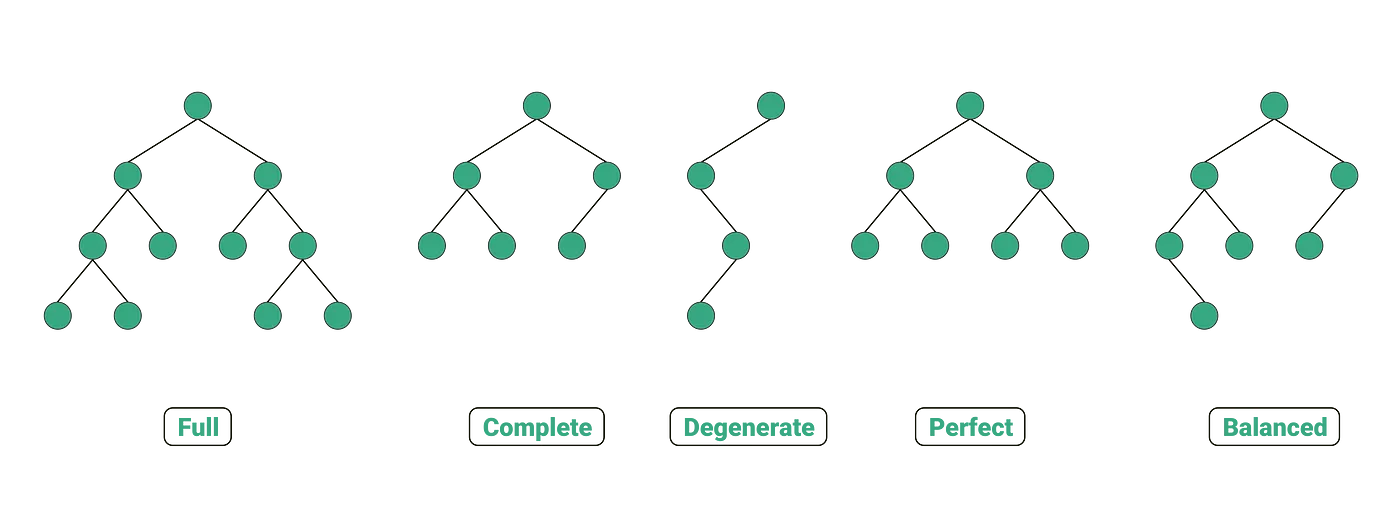

Fig. 15
Full Binary Tree is a Binary Tree in which every node has 0 or 2 children.
– towardsdatascience.com#

Fig. 16
Complete Binary Tree has all levels completely filled with nodes except the last level and in the last level, all the nodes are as left side as possible.
– towardsdatascience.com#
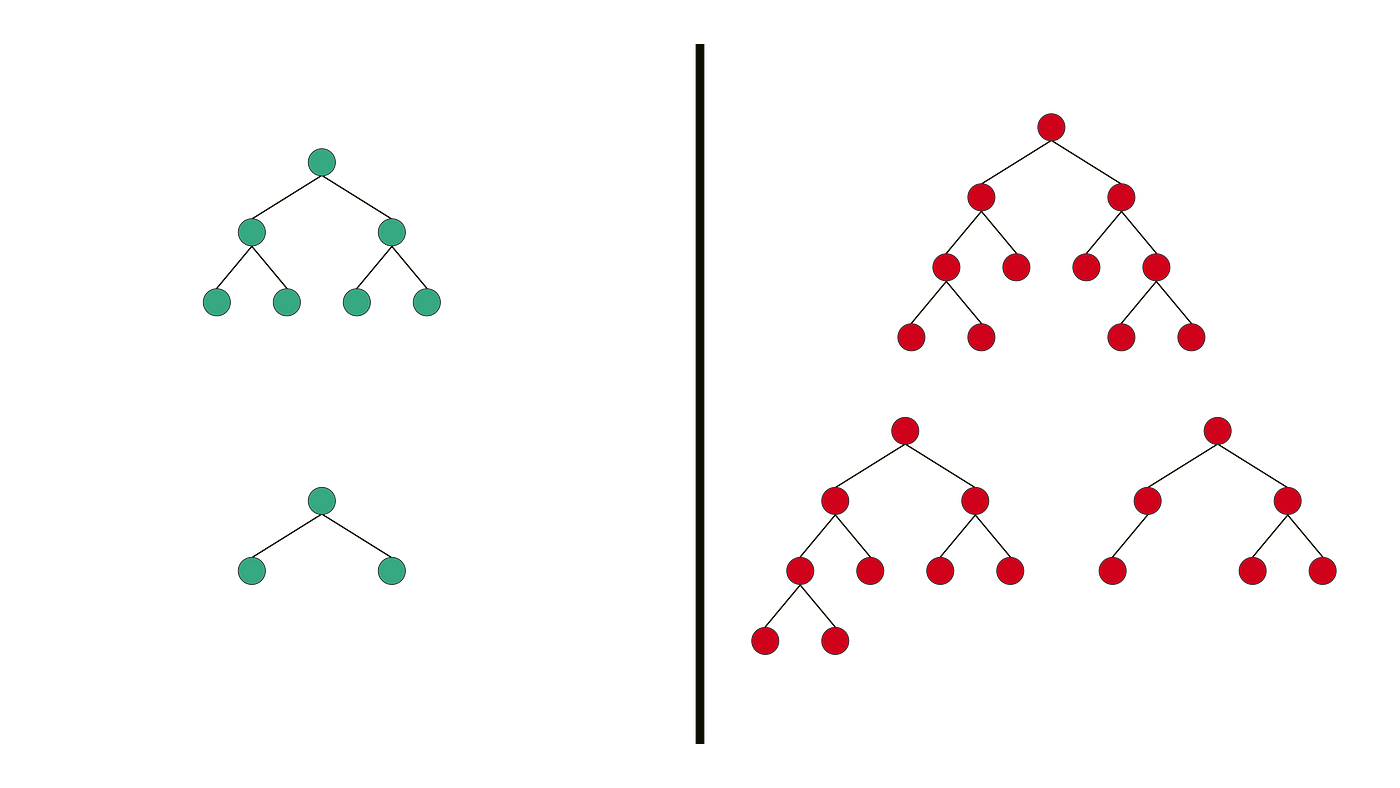
Fig. 17
Perfect Binary Tree is a Binary Tree in which all internal nodes have 2 children and all the leaf nodes are at the same depth or same level.
– towardsdatascience.com#

Fig. 18
Degenerate Binary Tree is a Binary Tree where every parent node has only one child node.
– towardsdatascience.com#
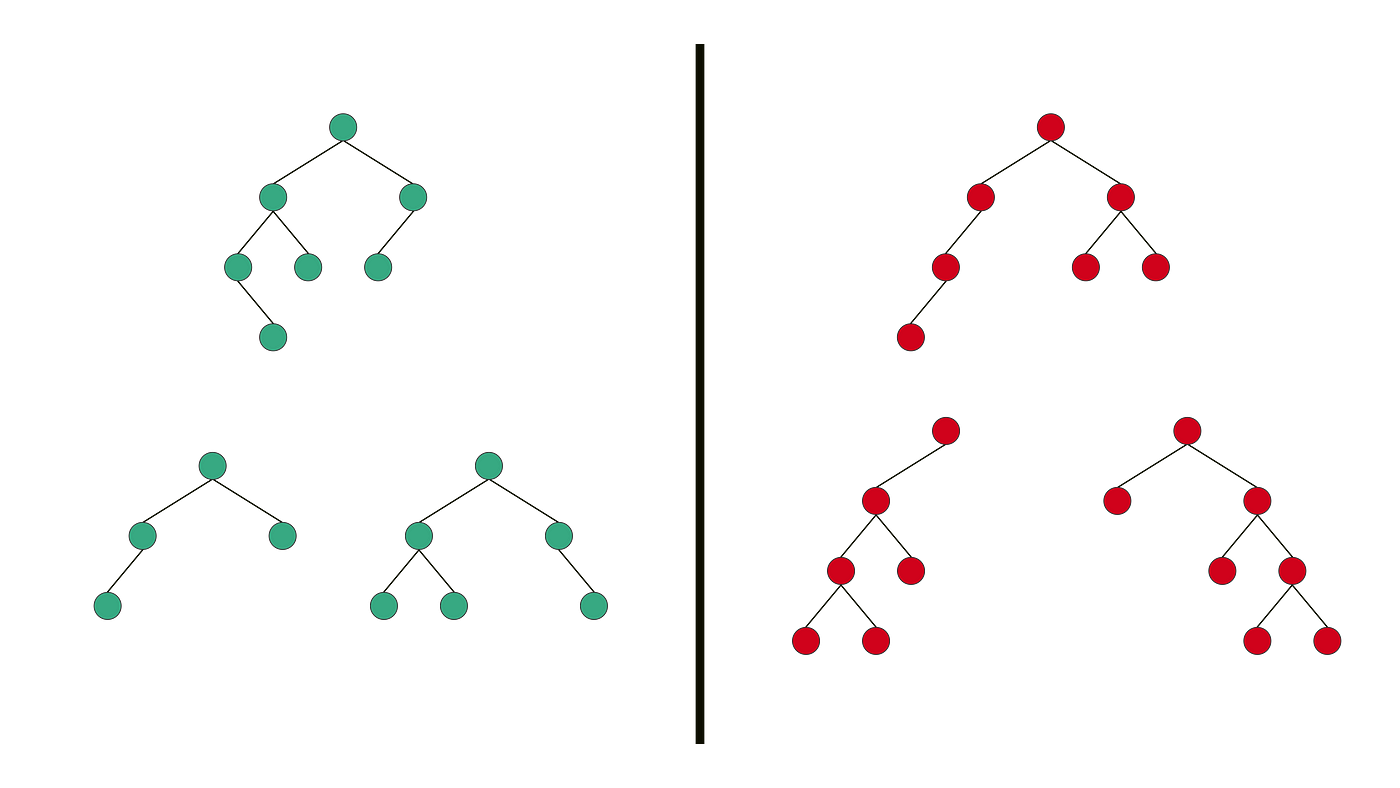
Fig. 19
Balanced Binary Tree is a Binary tree in which height of the left and the right sub-trees of every node may differ by at most 1.
– towardsdatascience.com#
Binary Search Trees#
Understanding BSTs
Each node in a binary tree can have at most two children.
This means that a node can have either zero, one, or two children.
The left child of a node is typically smaller than the node, while the right child is larger (or equal) than the node.
This rule is often associated with binary search trees (BSTs), where the values are arranged in a specific order for efficient searching and retrieval.
The order of children matters.
In a binary tree, the left child is typically referenced before the right child.
The order of children affects the tree’s traversal and interpretation.
Nodes are connected by edges.
The connections between nodes are represented by edges in a binary tree.
Each node (except the root) has exactly one incoming edge from its parent.
The height of a binary tree.
The height of a binary tree is the maximum number of edges from the root to a leaf node.
It represents the longest path from the root to any leaf node in the tree.
The depth (level) of a node.
The depth (or level) of a node in a binary tree represents the number of edges from the root to that node.
The root node is at depth 0, its children are at depth 1, and so on.
The number of nodes in a binary tree.
The total number of nodes in a binary tree can vary.
The minimum number of nodes in a binary tree is 0, while the maximum number depends on the height of the tree.
Simplified is bst
A BST has symmetric order
each node \(x\) in a BST has a key
for all nodes \(y\) in the left subtree of \(x\),
for all nodes \(y\) in the right subtree of \(x\),

(**) assume that the keys of a BST are pairwise distinct

BST Classes#
1class BSTNode {
2
3 private:
4 int data;
5 BSTNode *left;
6 BSTNode *right;
7
8 public:
9 BSTNode(int d);
10 ~BSTNode();
11
12 friend class BSTree;
13
14};
1class BSTree{
2
3 private:
4 BSTNode *root;
5 void destroy(BSTNode *p);
6
7 public:
8 BSTree();
9 ~BSTree();
10 void insert(int d);
11 void remove(int d);
12 BSTNode *search(int d);
13
14};
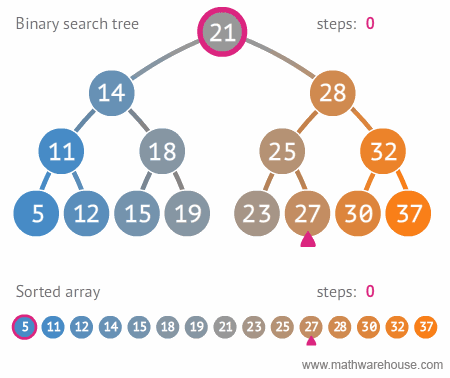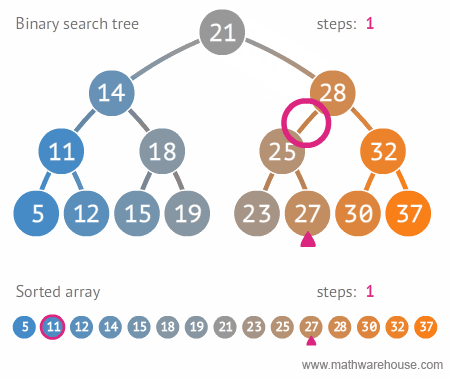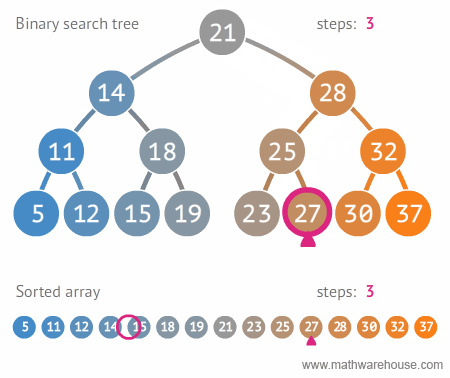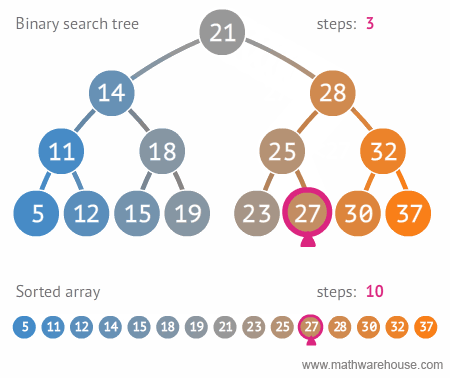
search#
Start at root node
If the search key:
a. matches the current node’s key
* then found
b. If search key \(>\) current node’s key
* search on \(right\) child
c. If search key is less than current node’s
* search on \(left\) childStop when current node is NULL (not found)

\(Search\ for\ \ 8\)
visualize
try it
insert#
To insert a new value into a BST:
Start at the root node.
If the value is smaller, go to the left subtree; if larger, go to the right subtree.
Repeat steps 2 until an empty spot is found.
Insert the new node in the empty spot.

visualize
try it
remove#
To delete a node from a BST:
Find the node to delete.
If the node has no children, simply remove it.
If the node has one child, replace it with its child.
If the node has two children, find the node’s successor (smallest value in the right subtree) or predecessor (largest value in the left subtree).
Replace the node with its successor/predecessor and delete the successor/predecessor from its original position.
Fig. 20 \(remove : leaf\)#
Fig. 21 \(remove:\ with\ 1\ child\)#
Fig. 22 \(remove:\ with\ 2\ children\)#
visualize
try it
Traversals#
Implications#
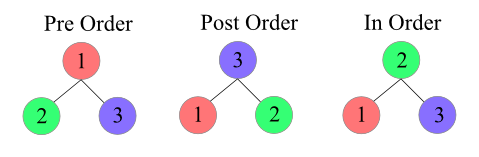
Traversal of a tree
Tis a systematic way of accessing, or “visiting,” all the positions ofT. The specific action associated with the “visit” of a positionpdepends on the application of this traversal, and could involve anything from incrementing a counter to performing some complex computation forp.
animation
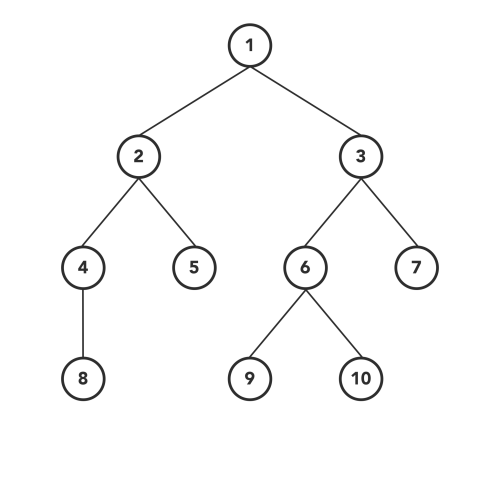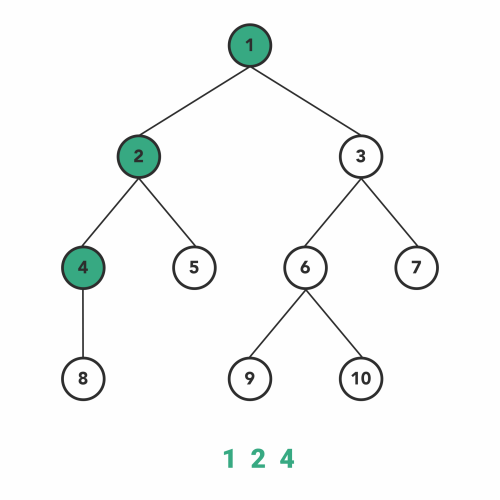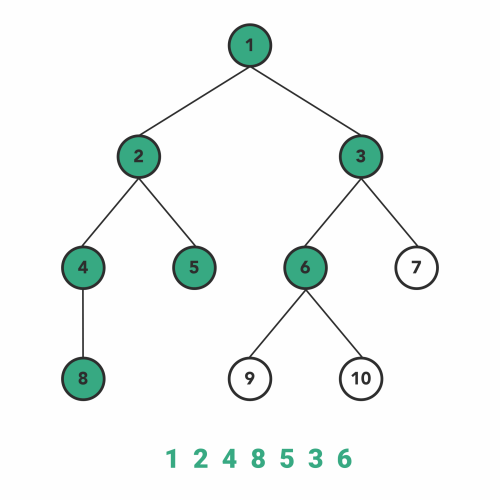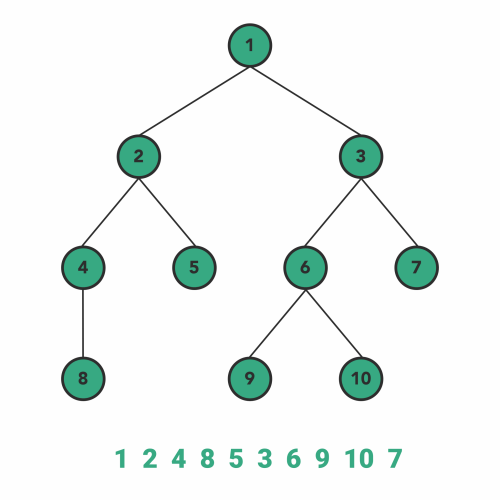
try it
animation

try it
How would we:
Destroy a binary tree
Post Order

Fig. 26
Post Order#
- Why?
It’s the only traversal that visits all the subtree nodes before visiting the root. All child nodes must be removed before we can delete the root.
Print all elements ascending order
In Order
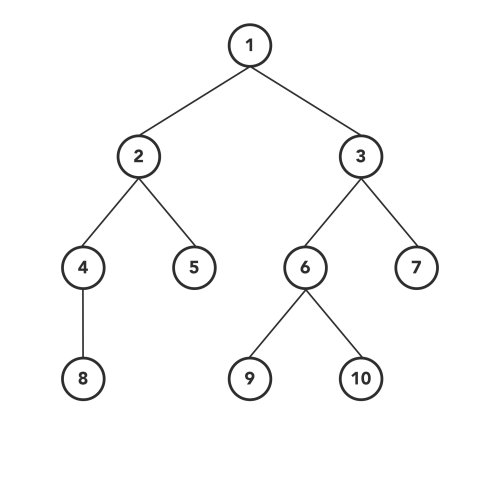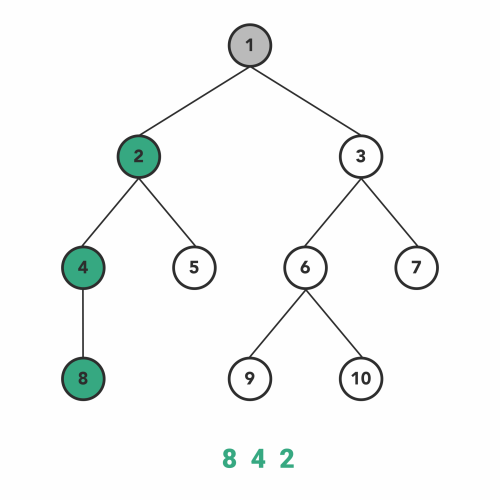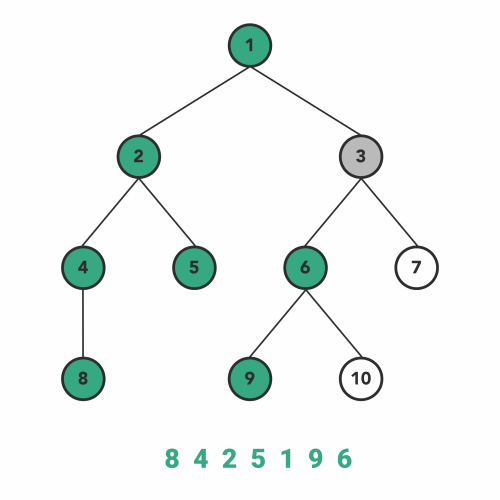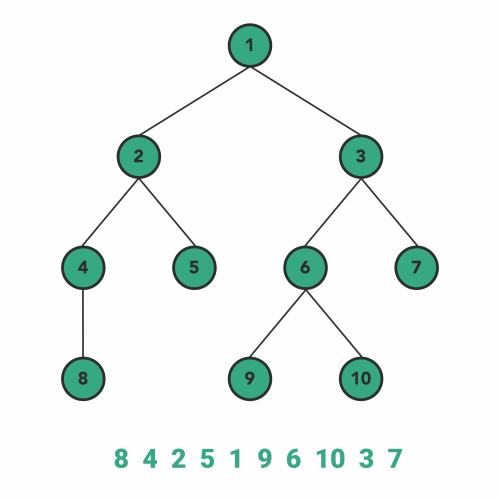
- Why?
to output in ascending order, we would need to start with the lowest value sequentially and work our way to the largest; as BST’s are built in sequential order, \(in-order\) fits best
best-case |
worst-case |
average-case |
|
|---|---|---|---|
search |
|||
insert |
|||
remove |
best-case |
worst-case |
average-case |
|
|---|---|---|---|
search |
\(O(1)\) |
\(O(n)\) |
\(O(log\ n)\) |
insert |
\(O(1)\) |
\(O(n)\) |
\(O(log\ n)\) |
remove |
\(O(log\ n)\) |
\(O(n)\) |
\(O(log\ n)\) |
Average-case analysis#
If \(n\) distinct keys are inserted into a BST in random order, expected number of compares for basic operations is
proof: 1-1 correspondence with quick-sort
Collections / Dictionaries#
What? |
Sequential (unordered) |
Sequential (ordered) |
BST |
|
|---|---|---|---|---|
search |
search for a key |
\(O(n)\) |
\(O(log\ n)\) |
\(O(h)\) |
insert |
insert a key |
\(O(n)\) |
\(O(n)\) |
\(O(h)\) |
delete |
delete a key |
\(O(n)\) |
\(O(n)\) |
\(O(h)\) |
min/max |
smallest/largest key |
\(O(n)\) |
\(O(1)\) |
\(O(h)\) |
floor/ceiling |
predecessor / successor |
\(O(n)\) |
\(O(log\ n)\) |
\(O(h)\) |
rank |
# of keys less than key |
\(O(n)\) |
\(O(log\ n)\) |
\(O(h)\)** |
(**) requires the use of ‘size’ at every node