Sets

Define

A set is a fundamental data structure in computer science that stores a collection of unique elements. It ensures that no duplicates are allowed, and it doesn’t impose a specific order on the elements.

An unordered_set is a fundamental data structure in computer science that represents a collection of unique elements, similar to a mathematical set. It is implemented as a hash table, providing fast access and ensuring uniqueness of its elements. Unlike a std::set, it does not maintain any specific order of the elements.

Use Cases

Graph Algorithms {both}

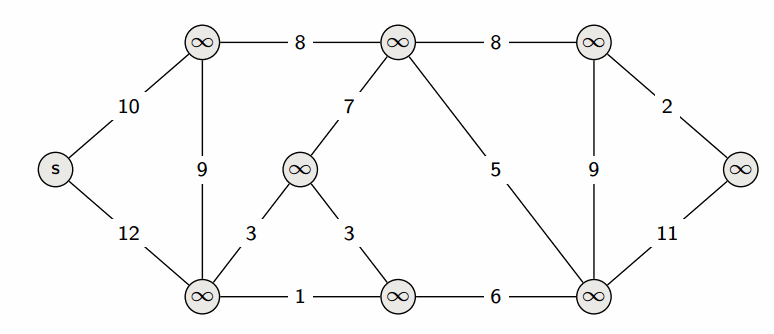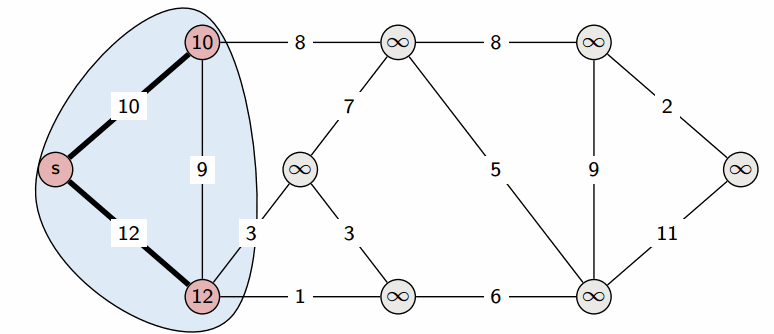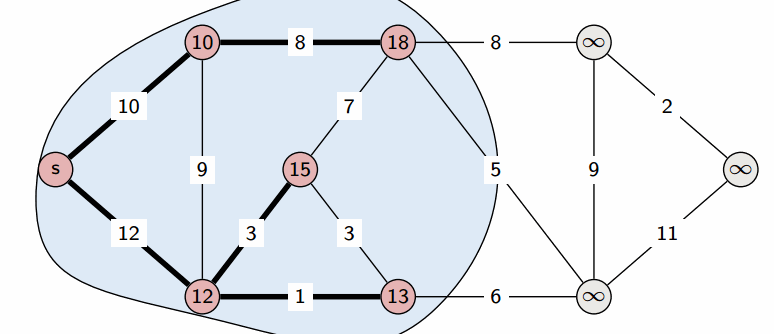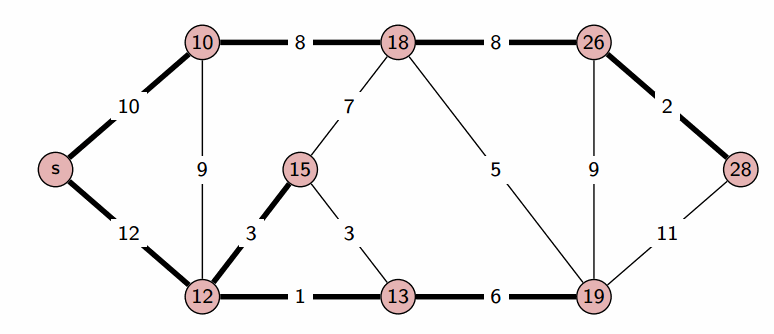
Sets can be used to track visited nodes in graph traversal algorithms.

Database Indexing {set}

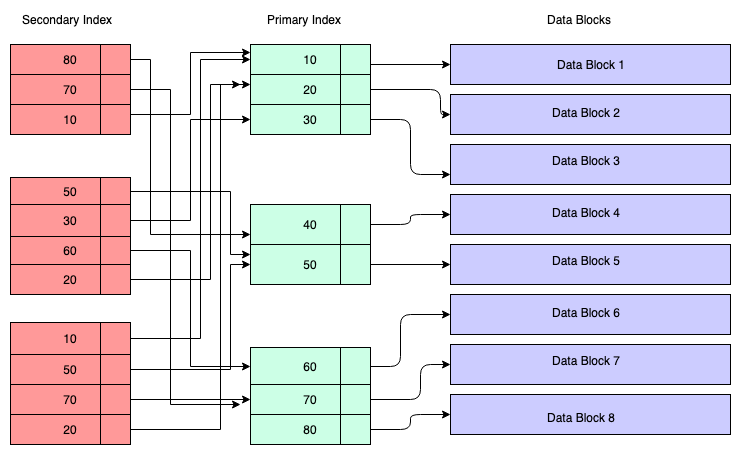
Sets are used to maintain unique values in database indexes, ensuring fast lookups.

Data Deduplication {unordered_set}

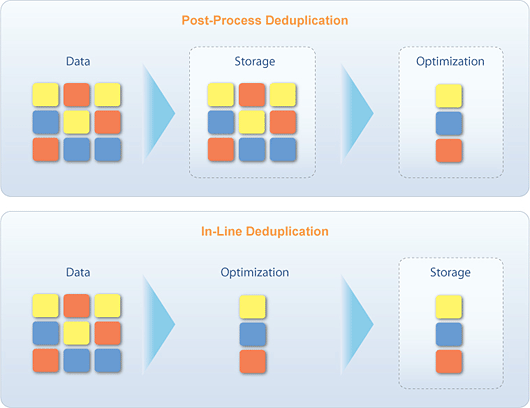
Removing duplicates from a list of records, such as emails or customer IDs.

Membership Testing {both}

Sets are efficient for checking whether an element is part of a specific group or category.

Spell Checking {set}

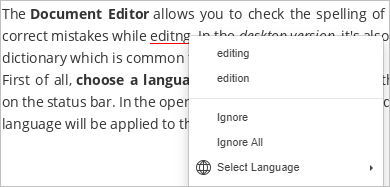
In word processing applications, a set can be used to maintain a dictionary of correctly spelled words.

Counting Occurrences {unordered_set}

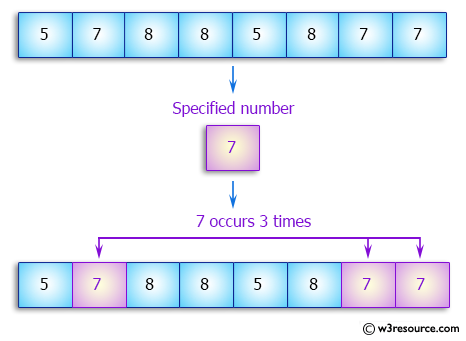
Counting the frequency of unique elements in a dataset.

Advantages & Disadvantages

Advantages

Uniqueness {both}

Sets enforce uniqueness, ensuring no duplicate elements.

Fast Lookup {both}

Efficient for searching and checking if an element exists.

Simple Interface {set}

Typically provides simple and intuitive methods like insert, contains, and remove.

Flexible Data Storage {unordered_set}

Suitable for scenarios where element order is not important.

Disadvantages

No Ordering {both}

Elements are not stored in a specific order, which may be a disadvantage in some use cases.

Overhead {set}

May require more memory and have some overhead for maintaining uniqueness.

Slower Insertions {set}

Inserting elements can be slower compared to data structures optimized for insertion.

Hash Collisions {unordered_set}

In rare cases, hash collisions can lead to performance degradation.

Programming

CppRef- set

Pseudo- set

Set Data Structure:
  - Initialize an empty set
  - Implement functions for insert, delete, search, and traverse

Code- set

We use the std::unordered_set container from the C++ Standard Library, which is a hash table-based implementation of a set.
We insert, check for existence, and remove elements using the insert, find, and erase methods.
Finally, we display the elements in the set.

#include <iostream>
#include <set>

int main() {
    std::set<int> mySet;
    
    // Insert elements
    mySet.insert(10);
    mySet.insert(5);
    mySet.insert(20);

    // Search for an element
    auto it = mySet.find(5);
    if (it != mySet.end()) {
        std::cout << "Element 5 found in the set.\n";
    }

    // Delete an element
    mySet.erase(10);

    // Traverse the set
    for (const int& element : mySet) {
        std::cout << element << " ";
    }
    std::cout << "\n";

    return 0;
}

Element 5 found in the set.
Set elements: 5 20

CppRef- unordered_set

Pseudo- unordered_set

Unordered Set Data Structure:

Data:
- Initialize an array (buckets) of a fixed size for storing elements.
- Each bucket is a linked list to handle collisions.

Functions:
- Insert(value):
    1. Calculate the hash of the value.
    2. Find the bucket using the hash.
    3. Search the bucket for the value; if not found, append the value to the bucket.

- Contains(value):
    1. Calculate the hash of the value.
    2. Find the bucket using the hash.
    3. Search the bucket for the value; return true if found, false otherwise.

- Remove(value):
    1. Calculate the hash of the value.
    2. Find the bucket using the hash.
    3. Search the bucket for the value, and if found, remove it.

- Display():
    1. Iterate through each bucket and display the elements.

Code- unordered_set

We use the std::unordered_set container from the C++ Standard Library, which is a hash table-based implementation of a set.
We insert, check for existence, and remove elements using the insert, find, and erase methods.
Finally, we display the elements in the set.

#include <iostream>
#include <unordered_set>

int main() {
    std::unordered_set<int> mySet;

    // Insert elements
    mySet.insert(10);
    mySet.insert(5);
    mySet.insert(20);

    // Check if an element exists
    if (mySet.find(5) != mySet.end()) {
        std::cout << "Element 5 found in the unordered set.\n";
    }

    // Remove an element
    mySet.erase(10);

    // Display the elements
    std::cout << "Unordered set elements: ";
    for (const int& element : mySet) {
        std::cout << element << " ";
    }
    std::cout << "\n";

    return 0;
}

Element 5 found in the unordered set.
Unordered set elements: 5 20

Compare

	std::set	std::unordered_set
Data Structure	Balanced Binary Search Tree	Hash Table
Order of Elements	Sorted, elements in ascending order	No specific order
find/contains	\(O(log\ n)\)	\(O(1)\) average, \(O(n)\) worst-case
insert	\(O(log\ n)\)	\(O(1)\) average, \(O(n)\) worst-case
remove	\(O(log\ n)\)	\(O(1)\) average, \(O(n)\) worst-case
Element Order	Preserved	No specific order
Memory Usage	Relatively lower	Relatively higher due to hash table
Custom Key Types	Requires operator< for keys	Requires a hash function
Range Iteration	Efficient	Less efficient
Use Cases	When elements need to be sorted	When fast access times are critical, order doesn’t matter
Extra Notes	Well-suited for maintaining sorted collections.	Suitable for fast access with no order requirement. Collision handling may degrade performance in rare cases.

Note: assume a well-designed/distributed hash function and minimal collisions. In practice, worst-case scenarios should also be considered, leading to amortized \(O(1)\) performance for many operations