Graphs : Breadth-First Search

TL;DR

Breadth-first search (BFS) is a graph traversal algorithm that visits all the vertices in a graph in level order, exploring all the vertices at a given distance from the starting vertex before moving on to vertices at a greater distance. BFS starts at a specified vertex (the starting vertex) and visits all its neighbors before visiting the neighbors of its neighbors, and so on.

BFS uses a queue data structure to keep track of the vertices that have been visited but not yet processed. The starting vertex is added to the queue, and then while the queue is not empty, the algorithm removes the first vertex from the queue, visits its neighbors, and adds them to the queue if they have not already been visited.

BFS can be used to perform a variety of operations on a graph, such as finding the shortest path between two vertices, checking whether the graph is connected, and identifying cycles in the graph.

BFS can be implemented using an iterative approach with a queue data structure, which is more memory-efficient than the recursive approach used in DFS.

Overall, BFS is an important algorithm in graph theory and is widely used in many applications, such as network analysis, data mining, and artificial intelligence.

Additional Resources

Breadth-first (in digraphs)

Shortest paths

Problem

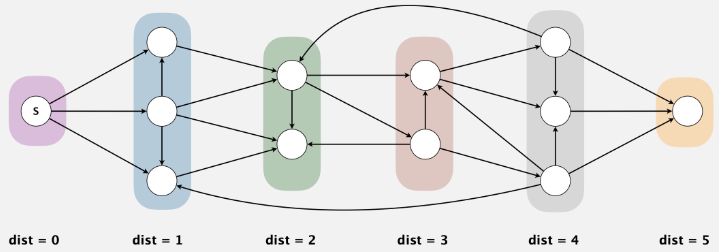
Find directed path from \(s\) to each other vertex that uses the fewest edges

Key idea

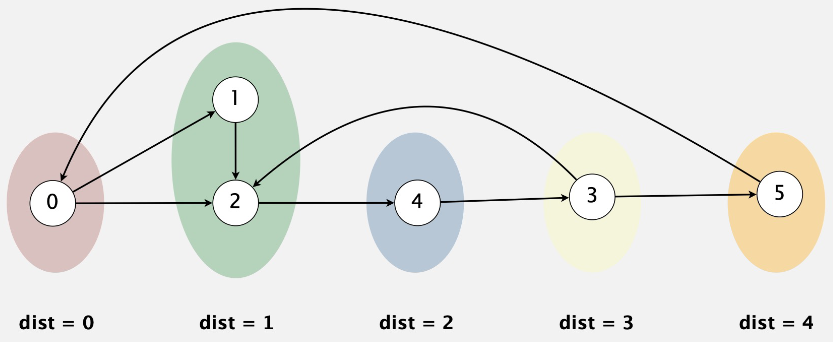
Visit vertices in increasing order of distance from \(s\)

Try writing some of the paths from 0 \(\Rightarrow\) 6

Click below to enter your path…

0 - 2 - 7 - 4 - 5 - 1 - 3 - 6

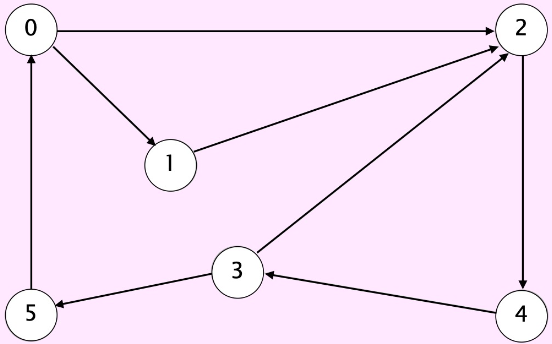
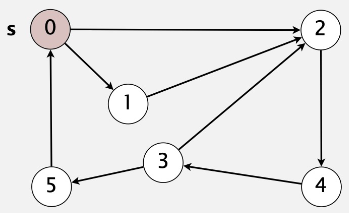
directed paths from \(0\) to \(6\)

\[0 \rightarrow 2 \rightarrow 7 \rightarrow 4 \rightarrow 5 \rightarrow 1 \rightarrow 3 \rightarrow 6 \]

\[0 \rightarrow 4 \rightarrow 5 \rightarrow 1 \rightarrow 3 \rightarrow 6 \]

\[0 \rightarrow 2 \rightarrow 7 \rightarrow 3 \rightarrow 6 \]

\[0 \rightarrow 2 \rightarrow 7 \rightarrow 0 \rightarrow 2 \rightarrow 7 \rightarrow 3 \rightarrow 6 \]

shortest path from \(0\) to \(6\ (length = 4)\)

\[0 \rightarrow 2 \rightarrow 7 \rightarrow 3 \rightarrow 6 \]

Key idea

Visit vertices in increasing order of distance from \(s\)

Key data structure

Queue of vertices to visit

BFS

Repeat until queue is empty

Remove vertex \(v\) from queue
Add to queue all unmarked vertices adjacent from \(v\) and mark them

BFS (from source s)
-----------------------------------------------
Add s to FIFO queue and mark s
Repeat until the queue is marked empty:
- remove the least recently added vertex
- for each unmarked vertex w adjacent from v:
  - add w to queue and mark w

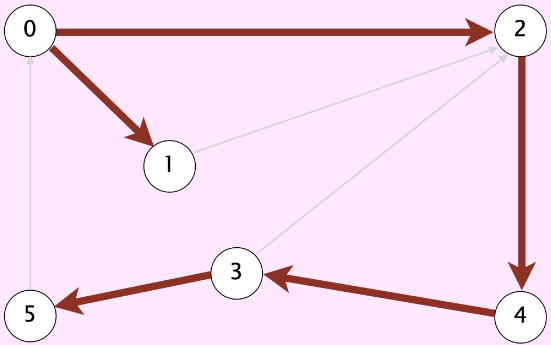
Fig. 83 graph g

Fig 58

\(v\)	\(edgeTo[]\)	\(marked[]\)	\(distTo[]\)
0	-	T	0
1	0	T	1
2	0	T	1
4	2	T	2
3	4	T	3
5	3	T	4

Properties

Proposition

In the worst case, BFS takes \(\Theta(E + V)\) time

Proof

Each vertex reachable from \(s\) is visited once

Fig. 84 digraph g

Fig. 85  

Ex 1

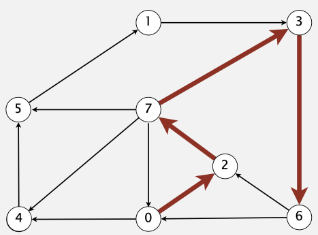
Single-sink Shortest Paths

Given a digraph and a target vertex \(t\), find shortest path from every vertex to \(t\)

Ex 1 \(t = 0\)

Shortest path from \(7\)

\(7 \rightarrow 6 \rightarrow 0\)

Shortest path from \(5\)

\(5 \rightarrow 4 \rightarrow 2 \rightarrow 0\)

Shortest path from \(12\)

\(12 \rightarrow 9 \rightarrow 11 \rightarrow 4 \rightarrow 2 \rightarrow 0\)

Ex 2

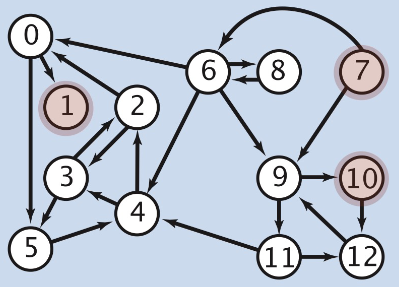
Multiple-source Shortest Paths

Given a digraph and a set of source vertices, find shortest path from any vertex in the set to every other vertex

Example \(S = \{ 1, 7, 10 \}\)

Shortest path to \(4\)

\(7 \rightarrow 6 \rightarrow 4\)

Shortest path to \(5\)

\(7 \rightarrow 6 \rightarrow 0 \rightarrow 5\)

Shortest path to \(12\)

\(10 \rightarrow 12\)

Breadth-first Search (in graphs)

Application: routing

Fewest number of hops in a communication network

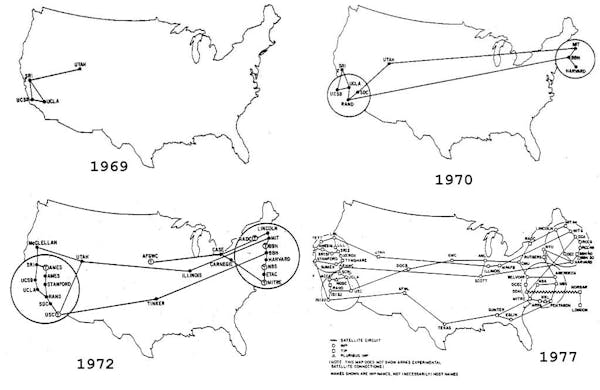
Fig. 86 ARPANET 1969 - 1977

BFS: undirected graphs

Problem

Find path between \(s\) and each other vertex that uses fewest edges

Solution

Treat as a digraph, replacing each undirected edge with two antiparallel edges

BFS (from source s)
-----------------------------------------------
Add s to FIFO queue and mark s
Repeat until the queue is empty:
- remove the least recently added vertex v
- for each unmarked vertex w adjacent from v:
  - add w to queue and mark w

Summary

Graph traversal

BFS and DFS enables efficient solution to many (but not all) graph and digraph problems

graph problem	BFS	DFS	time
s-t path	✔︎	✔︎	E + V
shortest s-t path	✔︎		E + V
shortest directed cycle	✔︎		E V
Euler cycle		✔︎	E + V
Hamilton cycle			\(2^{1.657 V}\)
bipartiteness	✔︎	✔︎	E + V
connected components	✔︎	✔︎	E + V
strong conmponents		✔︎	E + V
planarity		✔︎	E + V
graph morphism			\(2^{c\ ln^{3}\ V}\)