Priority Queues

Introduction

Queues & PQs

PQ Pt.1

PQ Pt.2

PQ Pt.3

PQ Pt.4

TL;DR

A priority queue is an abstract data type in computer science that stores a collection of elements with associated priorities, and provides operations for adding and removing elements in a way that respects their priorities.

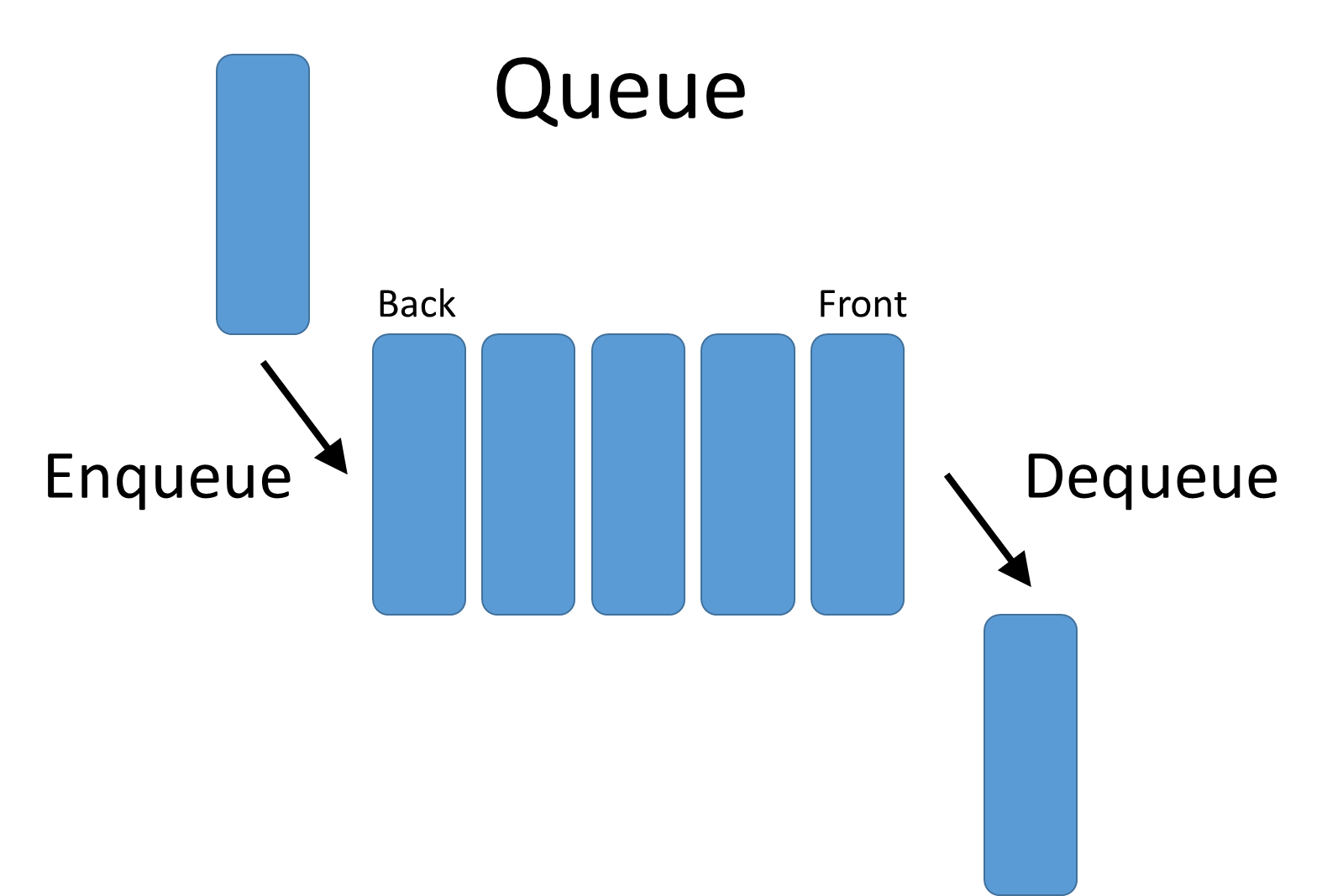
A priority queue is similar to a queue data structure, but unlike a queue, the order in which elements are removed from a priority queue is based on their priority rather than their order of insertion. In other words, the element with the highest priority is removed first, regardless of when it was added to the priority queue.

Priority queues are commonly used in applications where tasks or events have different levels of importance, such as task scheduling, event-driven simulations, and network routing protocols.

Priority queues can be implemented using various data structures, such as arrays, linked lists, heaps, and binary search trees. However, heap-based implementations are the most common, as they provide efficient \(O(log\ n)\) time complexity for both insertion and removal operations, making them suitable for large collections.

Definitions

Collections

Insert and delete items. Which items to delete?

Stack

Remove the item most recently added

Generalizes

stack, queue, randomized queue

Queue

Remove the item least recently added

Randomized Queue

Remove a random item

Priority Queue

Remove the largest (or smallest) item

Queue & Priority Queue

Q

Fig. 10 Queues

PQ

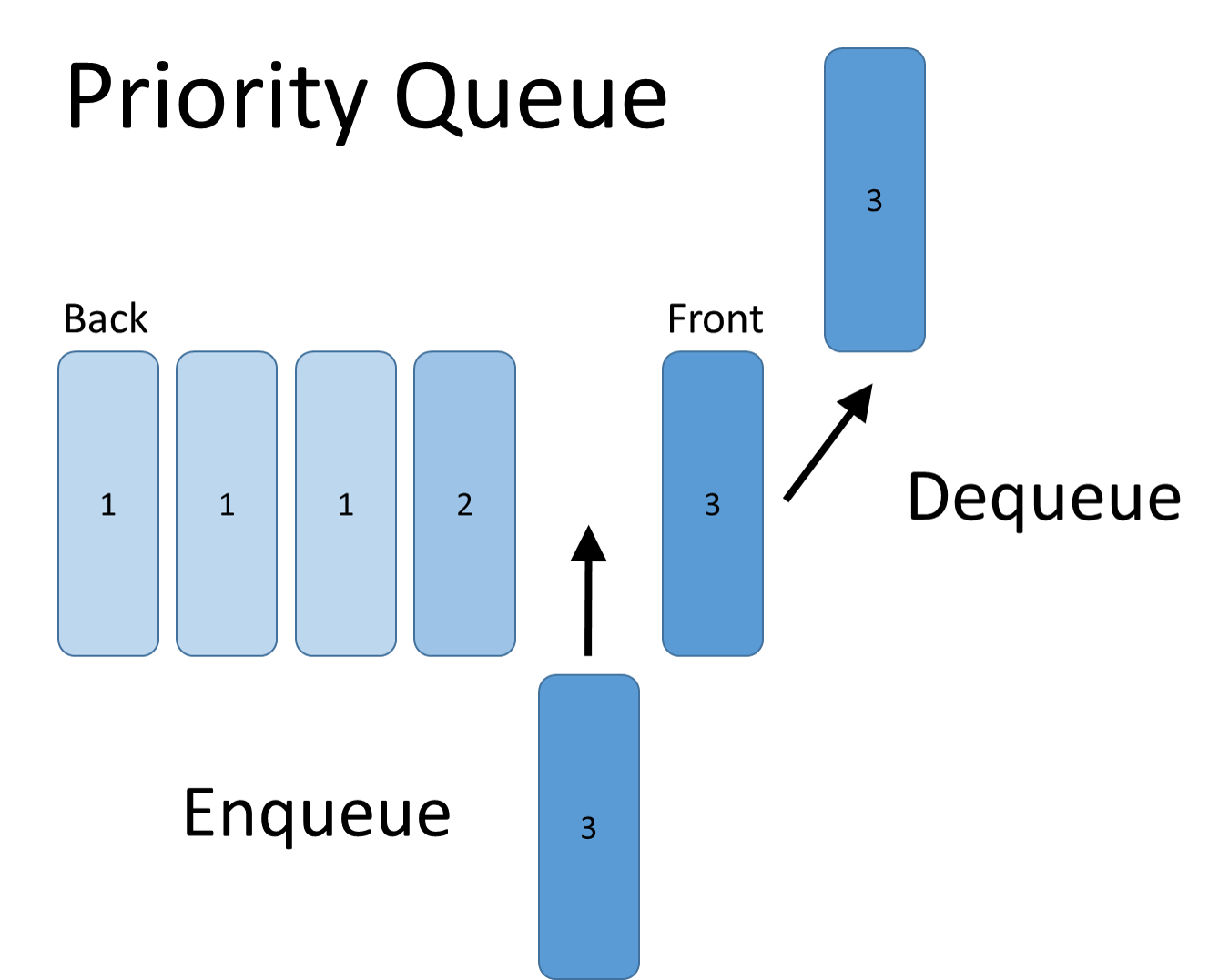
Fig. 11 Priority Queue

Applications

Data compression in Huffman code

Network Routing

CPU Scheduling

Other examples…

• Artificial Intelligence (search)

• Graph Algorithms

• Stream Data Algorithms

• HPC Task Scheduling

• Graph algorithms like Dijkstra’s shortest path algorithm, Prim’s Minimum Spanning Tree, etc.

• Stack Implementation

• All queue applications where priority is involved.

• Event-driven simulation such as customers waiting in a queue.

• Finding Kth largest/smallest element.

Priority Queues

Collections of \(<key, value>\) pairs

• keys are objects on which an order is defined

Every pair of keys must be comparable according to a total order:

Properties

Reflexive

\[k_1 \le k_2\]

Antisymmetric

\[k_1 \le\ k_2 \ \ \ \land \ \ \ k_2 \le k_1\]

\[\Rightarrow\]

\[k_1 = k_2\]

Transitive

\[k_1 \le k_2 \ \ \ \land \ \ \ k_2 \le k_3\]

\[\Rightarrow\]

\[k_1 \le k_3\]

Queues

• basic operations:

  • \(enqueue\), \(dequeue\)

• always remove the item least recently added

Priority Queues

• basic operations:

  • \(insert\), \(removeMax\)

• MaxPQ:

  • always remove the item with the highest (max) priority

• MinPQ:

  • always remove the item with the lowest (min) priority

Fig. 12 Working with PQ’s

Performance

	Sorted Array/List	Unsorted Array/List
insert	\(O(n)\) must find place where to insert item	\(O(1)\) item can be inserted at head or tail
removeMax max	\(O(1)\) largest/smallest key is at: \(arr[0]\)/\(arr[n-1]\)	\(O(n)\) must traverse entire sequence to find largest/smallest

cppreference.com

Implementations

Arrays	enqueue \(O(1)\)	dequeue \(O(n)\)	peek \(O(n)\)
Linked List	push \(O(n)\)	pop \(O(1)\)	peek \(O(1)\)
Binary Heap	insert \(O(log\ n)\)	remove \(O(log\ n)\)	peek \(O(1)\)
Binary Tree	insert \(O(log\ n)\)	delete \(O(log\ n)\)	peek \(O(1)\)

Note: assume all collections are unsorted…

Advantages & Disadvantages

Advantages

Faster elemental access

This is because elements in a priority queue are ordered by priority, one can easily retrieve the highest priority element without having to search through the entire queue.

Dynamic ordering

Elements in a priority queue can have their priority values updated, which allows the queue to dynamically reorder itself as priorities change.

Efficient algorithms can be implemented

Priority queues are used in many algorithms to improve their efficiency, such as Dijkstra’s algorithm for finding the shortest path in a graph and the A* search algorithm for pathfinding.

Included in real-time systems

This is because priority queues allow you to quickly retrieve the highest priority element, they are often used in real-time systems where time is of the essence.

Disadvantage

High complexity

Priority queues are more complex than simple data structures like arrays and linked lists, and may be more difficult to implement and maintain.

High consumption of memory

Storing the priority value for each element in a priority queue can take up additional memory, which may be a concern in systems with limited resources.

Not always the most efficient data structure

In some cases, other data structures like heaps or binary search trees may be more efficient for certain operations, such as finding the minimum or maximum element in the queue.

Less predictable at times

This is because the order of elements in a priority queue is determined by their priority values, the order in which elements are retrieved may be less predictable than with other data structures like stacks or queues, which follow a first-in, first-out (FIFO) or last-in, first-out (LIFO) order.