Heapsort

HeapSort

Definition

A heap`` is a specialized binary tree-based data structure that satisfies the heap property. In the context of sorting, a heap`` usually refers to a binary heap. A binary heap is a complete binary tree where the parent node’s value is either greater than or less than its children, depending on whether it’s a max-heap or a min-heap. In the case of heap sort, a max-heap is often used, where the largest element is at the root.

Advantages & Disadvantages

Advantages

\(O(n * log(n))\)

• making it efficient for large datasets

In-place sorting

• doesn’t require additional memory

Disadvantages

Not stable

• Equal elements can be rearranged during the sorting process

Slower

• …for small datasets compared to some other sorting algorithms.

\(O(n * log(n))\)

• Worst / Average Case complexity the same…

Programming

General

Conceptual

Pseudocode

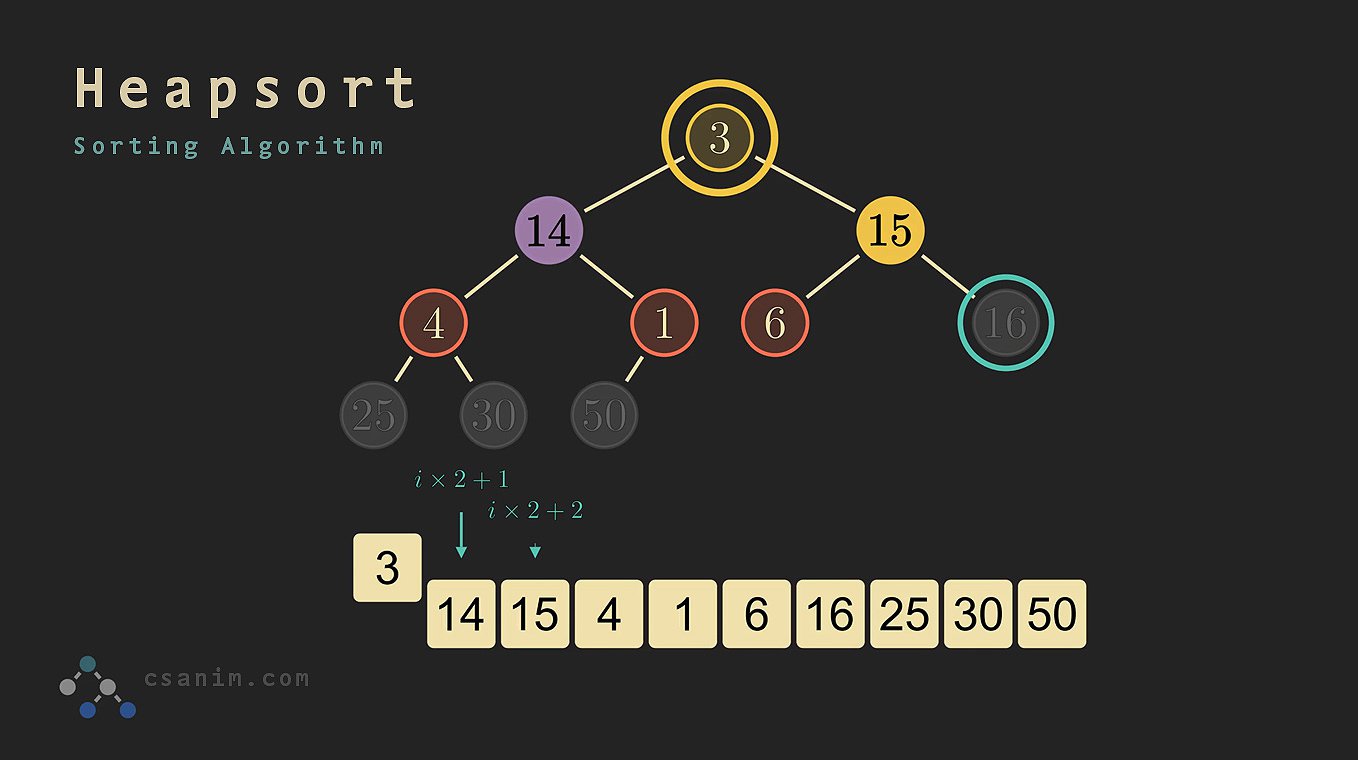
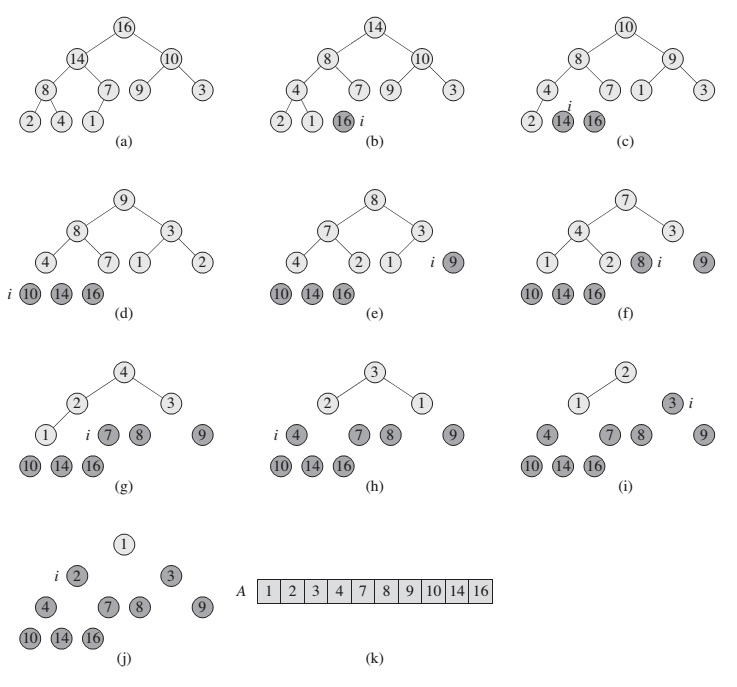
HeapSort(arr):
    BuildMaxHeap(arr)  // Build a max heap from the array.
    for i from n down to 2:  // n is the size of the array.
        Swap arr[1] and arr[i]  // Move the maximum element to the end.
        Heapify(arr, 1, i-1)  // Restore the max-heap property.

BuildMaxHeap(arr):
    for i from n/2 down to 1:
        Heapify(arr, i, n)

Heapify(arr, i, n):
    largest = i
    left = 2 * i
    right = 2 * i + 1
    if left ≤ n and arr[left] > arr[largest]:
        largest = left
    if right ≤ n and arr[right] > arr[largest]:
        largest = right
    if largest ≠ i:
        Swap arr[i] and arr[largest]
        Heapify(arr, largest, n)

C++

#include <iostream>

// Function to heapify a subtree rooted at index i.
void heapify(int arr[], int n, int i) {
    int largest = i;
    int left = 2 * i + 1;
    int right = 2 * i + 2;

    if (left < n && arr[left] > arr[largest])
        largest = left;

    if (right < n && arr[right] > arr[largest])
        largest = right;

    if (largest != i) {
        std::swap(arr[i], arr[largest]);
        heapify(arr, n, largest);
    }
}

// The main function to perform heap sort.
void heapSort(int arr[], int n) {
    // Build a max-heap.
    for (int i = n / 2 - 1; i >= 0; i--)
        heapify(arr, n, i);

    // Extract elements one by one from the heap.
    for (int i = n - 1; i > 0; i--) {
        std::swap(arr[0], arr[i]);  // Move current root to end.
        heapify(arr, i, 0);  // Call max heapify on the reduced heap.
    }
}

int main() {
    int arr[] = {12, 11, 13, 5, 6, 7};
    int n = sizeof(arr) / sizeof(arr[0]);

    heapSort(arr, n);

    std::cout << "Sorted array is: ";
    for (int i = 0; i < n; i++)
        std::cout << arr[i] << " ";

    return 0;
}

Real World Use Cases

Heap sort may not be directly used in real-world applications, but the heap data structure itself has various applications. For example:

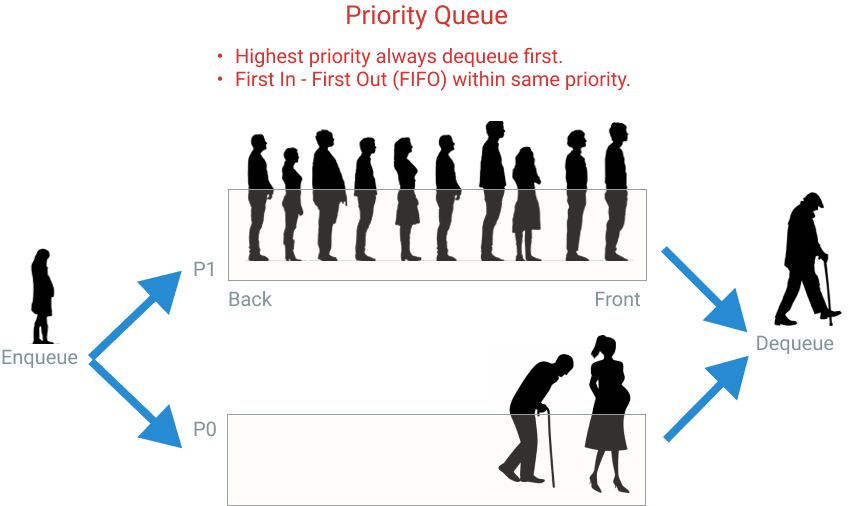
Priority Queues

Heaps are used to efficiently implement priority queues, which are essential in various scheduling algorithms and simulations.

Dijkstra’s Algorithm

It employs a min-heap to find the shortest path in a graph.

Memory Management

Heaps are used in memory management systems to allocate and de-allocate memory efficiently.