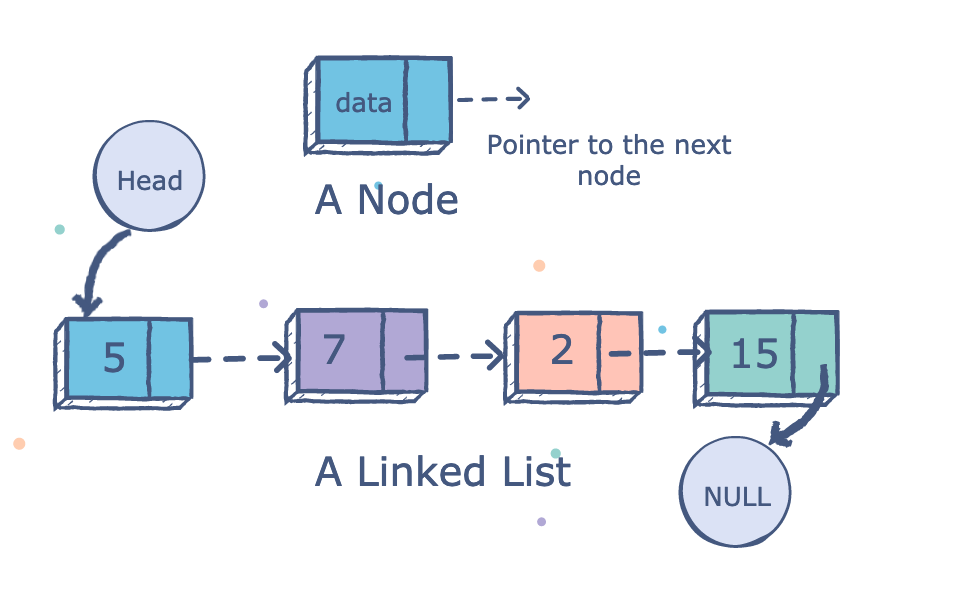
Hash Tables#

TL;DR

A hash table is a data structure that provides efficient insertion, deletion, and lookup operations on key-value pairs. It works by using a hash function to map each key to a position in an array, called the hash table, where the corresponding value is stored.

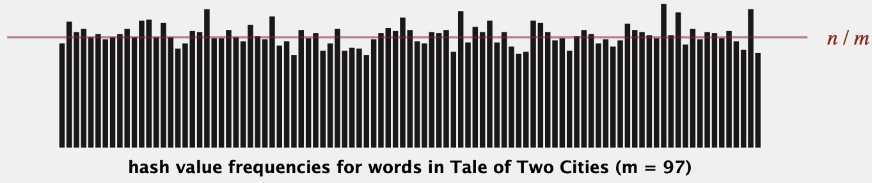
The hash function takes a key as input and generates a hash code, which is used to determine the position in the array where the value should be stored. Ideally, the hash function should distribute the keys uniformly across the hash table, to minimize collisions (i.e., when two or more keys map to the same position in the array).

To handle collisions, a hash table typically uses a collision resolution strategy, such as chaining or open addressing. Chaining involves storing all the values that hash to the same position in a linked list, while open addressing involves finding the next available position in the array to store the value.

One of the advantages of hash tables is their speed. In the average case, operations on a hash table have a constant-time complexity of \(O(1)\), meaning that the time taken to perform an operation does not depend on the size of the hash table. This makes hash tables ideal for applications where fast lookup and insertion times are important.

Overall, hash tables are an important data structure in computer science, and are widely used in applications such as databases, compilers, and web servers. However, the efficiency of hash tables depends on the quality of the hash function used, and collisions can still occur, which can degrade performance.

Additional Resources

Storing data#

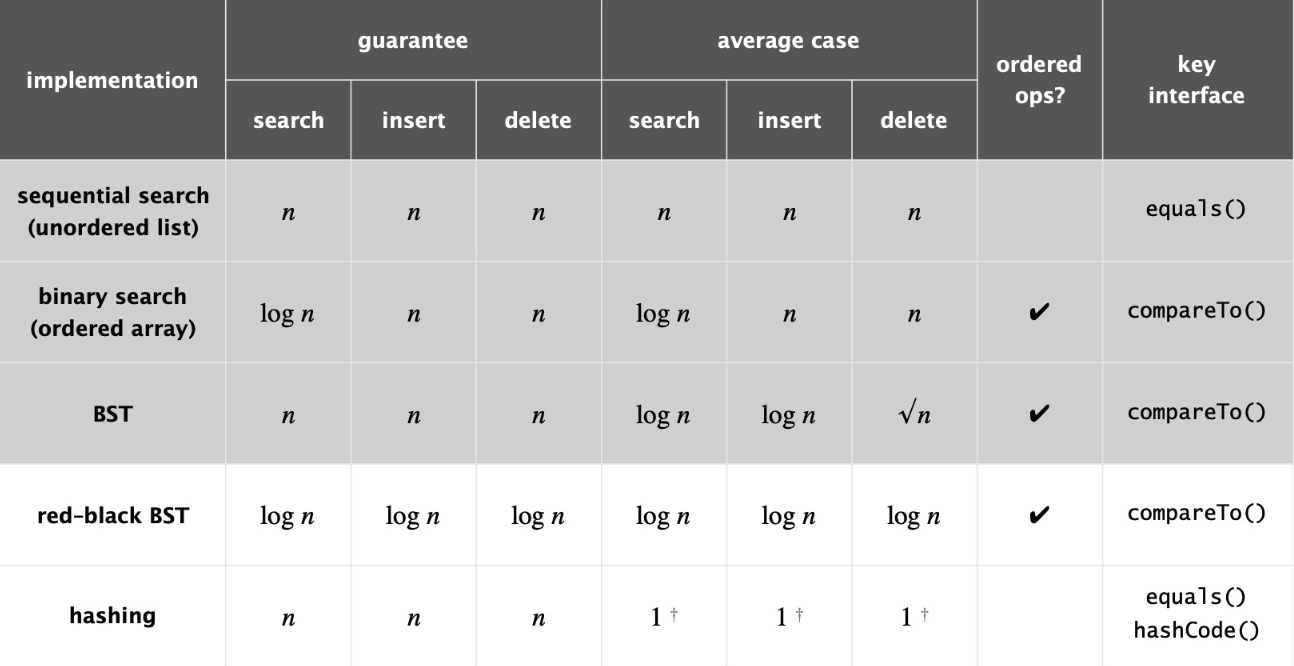
../../_images/18_00.png

Fig. 66 Summary Table#

Hash Tables#

  • implements an associative array or dictionary

  • an abstract data type that maps keys to values

  • uses a hash function to compute an \(index\), also called a \(hash code\)

  • at lookup, the key is hashed and the resulting hash indicates where the corresponding value is stored.

https://s3.ap-south-1.amazonaws.com/s3.studytonight.com/tutorials/uploads/pictures/1604593128-76844.png

Fig. 67 Hash Table#

Why not…#

Arrays & Linked Lists
https://miro.medium.com/max/970/1*f2oDQ0cdY54olxCFOIMIdQ.png

  • Search \(O(log\ n)\)

  • Insert/Delete, much more costly

Balanced BST
https://media.geeksforgeeks.org/wp-content/cdn-uploads/BinaryTree3-300x188.png

  • Guarenteed \(O(log\ n)\)

Direct Access Table
https://www.kindsonthegenius.com/wp-content/uploads/2020/09/Direct-Address-Table-1.jpg

  • Best-case \(O(1)\)

  • Practical limitations

    • Extra space

    • A given integer in a programmming language may not store \(n\) digits

    • Therefore, not always a viable option

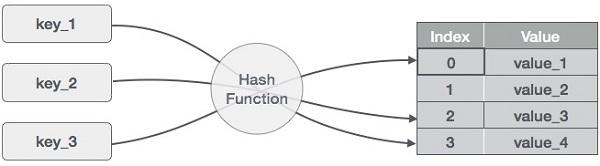
Hash Functions#

  • a function converting a piece of data into a smaller, more practical integer

  • the integer value is used as the \(index\) between 0 and \(m-1\) for the data in the hash table

  • ideally, maps all keys to a unique slot \(index\) in the table

  • perfect hash functions may be difficult, but not impossible to create

https://www.vladimircicovic.com/content/images/20200502181417-hash_function.jpg
Properties of good hash functions

  • Efficiently computable

  • Should uniformly distribute the keys (each table position equally likely for each)

  • Should minimize collisions

  • Should have a low load factor \(\frac{\#\ items\ in\ table}{table\ size}\)

Modular Hashing#

To uniformly create hashes, hash functions may use heuristic techniques of division or multiplication
Legend

\(h\) = hash function
\(x\) = key
\(HT\) = hash table
\(m\) = table size
\(b\) = buckets
\(r\) = items per bucket

Rules
\[\begin{split}\begin{align} 0 \le h(x) \lt m\ , or \\ 0 \le h(x) \lt b-1 \end{align}\end{split}\]
\[Entry\ lookup \Rightarrow HT[h(x)]\]
Syntax
\[\begin{split}\begin{align} h(x) & = x\ mod\ m \\ & = x\ \%\ m \end{align}\end{split}\]
Example

Suppose there are six students:

\(a1, a2, a3, a4, a5, a6\) in the Data Structures class and their IDs are:

\[\begin{split}\begin{align} a1: & 197354863; \\ a2: & 933185952; \\ a3: & 132489973; \\ a4: & 134152056; \\ a5: & 216500306; \\ a6: & 106500306. \\ \end{align}\end{split}\]
Hashing
\[h: \{k_1,k_2,k_3,k_4,k_5,k_6 \} \rightarrow \]
\[ \ \ \ \ \{0,1,2,...12\}\ by\ h(k_1) = k_1 \%\ 13\]
\[\begin{split}\begin{align} h(k_1) & = 197354863\ \ \%\ 13 = 4 \\ h(k_2) & = 933185952\ \ \%\ 13 = 10 \\ h(k_3) & = 132489973\ \ \%\ 13 = 5 \\ h(k_4) & = 134152056\ \ \%\ 13 = 12 \\ h(k_5) & = 216500306\ \ \%\ 13 = 9 \\ h(k_6) & = 106500306\ \ \%\ 13 = 3 \\ \end{align}\end{split}\]
Outcome

Suppose \(HT[b] \leftarrow a\)…

\[\begin{split}\begin{align} HT[4] \leftarrow 197354863 \\ HT[5] \leftarrow 132489973 \\ HT[9] \leftarrow 216500306 \\ HT[10] \leftarrow 933185952 \\ HT[12] \leftarrow 134152056 \\ HT[3] \leftarrow 106500306 \\ \end{align}\end{split}\]

Uniform Hashing#

Assumption#

Any key is equally likely (and independent of other keys) to hash to one of \(m\) possible indices

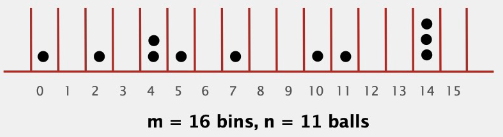
Bins and Balls#

Toss \(n\) balls uniformly at random into \(m\) bins

Bad News [birthday problem]#

In a random group of 23 people, more likely than not that two people share the same birthday Expect two balls in the same bin after \(\sim \sqrt{\pi * \frac{m}{2}} \ \ \ \ \ \ \ \ \ \ // = 23.9\ when\ m = 365\)

Good News#

when \(n \gt\gt m\), expect most bins to have \(\approx \frac{n}{m}\) balls when \(n = m\), expect most loaded bin has \(\sim \frac{ln\ n}{ln\ ln\ n}\) balls

../../_images/18_04.png
../../_images/18_05.png

Collisions#

Two distinct keys that hash to the same index birthday problem

\(\Rightarrow\) can’t avoid collisions

load balancing

\(\Rightarrow\) no index gets too many collisions
\(\Rightarrow\) ok to scan though all colliding keys

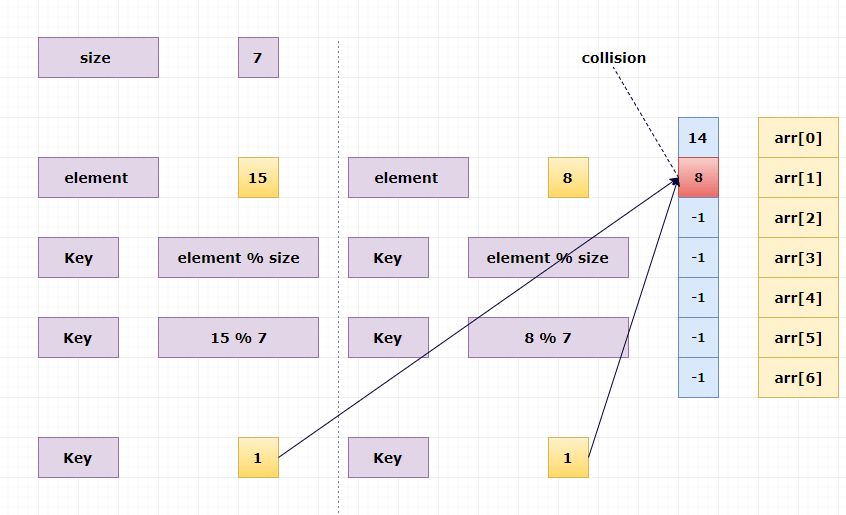
https://www.log2base2.com/images/algo/hash-collision.png

Fig. 68 collision#

Separate Chaining#

Simple Uniform Hashing

  • keeps a list of all elements that hash to the same value

Performance

\(m\) = Number of slots in hash table
\(n\) = Number of keys to be inserted in hash table

Load factor \(α = n/m\)
Expected time to search or delete = \(O(1 + α)\)

Time to insert = \(O(1)\)
Time complexity of search, insert, and delete is \(O(1)\ if\ α\ is\ O(1)\)

Example

Example
\[h : {0,81,64,25,36,49,1,4,16,9}\]

\(h(k_1) = 0\ \ \ \ \%\ 10 = 0\ \ \ \ \ \ \ \Rightarrow\ \ \ \ \ HT[0] \leftarrow 0\)
\(h(k_2) = 81\ \ \%\ 10 = 1\ \ \ \ \ \ \ \Rightarrow\ \ \ \ \ HT[1] \leftarrow 81\)
\(h(k_3) = 64\ \ \%\ 10 = 4\ \ \ \ \ \ \ \Rightarrow\ \ \ \ \ HT[4] \leftarrow 64\)
\(h(k_4) = 25\ \ \%\ 10 = 5\ \ \ \ \ \ \ \Rightarrow\ \ \ \ \ HT[5] \leftarrow 25\)
\(h(k_5) = 36\ \ \%\ 10 = 6\ \ \ \ \ \ \ \Rightarrow\ \ \ \ \ HT[6] \leftarrow 36\)
\(h(k_6) = 49\ \ \%\ 10 = 9\ \ \ \ \ \ \ \Rightarrow\ \ \ \ \ HT[9] \leftarrow 49\)
\(h(k_7) = 1\ \ \ \ \%\ 10 = 1\ \ \ \ \ \ \ \Rightarrow\ \ \ \ \ HT[1] \leftarrow 1\)
\(h(k_8) = 4\ \ \ \ \%\ 10 = 4\ \ \ \ \ \ \ \Rightarrow\ \ \ \ \ HT[4] \leftarrow 4\)
\(h(k_9) = 16\ \ \%\ 10 = 6\ \ \ \ \ \ \ \Rightarrow\ \ \ \ \ HT[6] \leftarrow 16\)
\(h(k_{10}) = 9\ \ \ \%\ 10 = 9\ \ \ \ \ \ \ \Rightarrow\ \ \ \ \ HT[9] \leftarrow 9\)

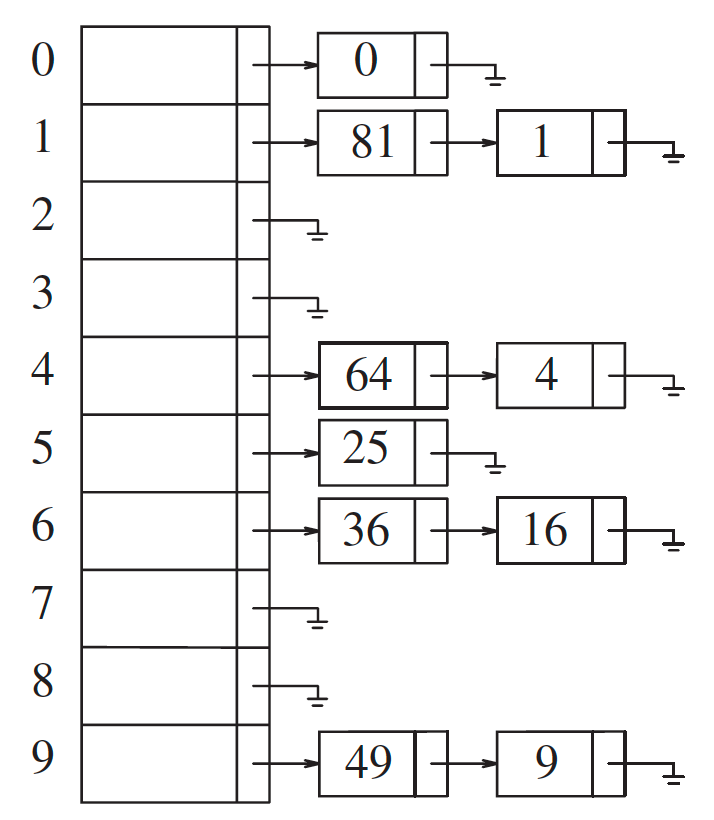
../../_images/18_06.png

Fig. 69 A separate chaining hash table#

Advantages / Disadvantages??
Advantages

  • Simple to implement.

  • Hash table never fills up, we can always add more elements to the chain.

  • Less sensitive to the hash function or load factors.

  • It is mostly used when it is unknown how many and how frequently keys may be inserted or deleted.

Disadvantages

  • The cache performance of chaining is not good as keys are stored using a linked list. Open addressing provides better cache performance as everything is stored in the same table.

  • Wastage of Space (Some Parts of the hash table are never used)

  • If the chain becomes long, then search time can become O(n) in the worst case

  • Uses extra space for links

Open Addressing#

Linear Probing

  • keeps a list of all elements that hash to the same value

Rule

\(h_i(x) = (Hash(x) + i) \ \% \ HashTableSize\)

If \(h_0(x) = (Hash(x) + 0) \ \% \ HashTableSize\)
If \(h_1(x) = (Hash(x) + 1) \ \% \ HashTableSize\)
If \(h_2(x) = (Hash(x) + 2) \ \% \ HashTableSize\)
… and so on

https://media.geeksforgeeks.org/wp-content/cdn-uploads/gq/2015/08/openAddressing1.png
Example
\[h : \{50, 700, 76, 85, 92, 73, 101\}\]
\[\begin{split}\begin{align} h_0(50) &= 50\ \ \ \ \% \ 7 = 1 \\ \\ h_0(700) & = 700\ \ \% \ 7 = 0 \\ \\ h_0(76) &= 76\ \ \ \% \ 7 \ = 6 \\ \\ \end{align}\end{split}\]
\[\begin{split}\begin{align} h_0(85) &= 85\ \ \ \% \ 7 \ = \color{red}{1} \\ & \Rightarrow h_1(85) = (85+1)\ \ \%\ 7 = 2 \\ h_0(92) &= 92\ \ \%\ 7 = \color{red}{1} \\ & \Rightarrow h_1(92) = (92+1)\ \ \%\ 7 = \color{red}{2} \\ & \Rightarrow h_2(92) = (92+2)\ \ \%\ 7 = 3 \\ \\ h_0(73) &= 73\ \ \%\ 7 = \color{red}{3} \\ & \Rightarrow h_1(73) = (73+1)\ \ \%\ 7 = 4 \\ \\ h_0(101) &= 101\ \ \%\ 7 = \color{red}{3} \\ & \Rightarrow h_1(101) = (101+1)\ \ \%\ 7 = \color{red}{4} \\ & \Rightarrow h_2(101) = (101+2)\ \ \%\ 7 = 5 \\ \end{align}\end{split}\]

Quadratic Probing#

Rule
\[\begin{split}\begin{align} h_i(x) & = (Hash(x) + i^2)\ \%\ \ HashTableSize \\ & \Rightarrow (Hash(x) + i*i)\ \%\ \ HashTableSize \\ \\ If\ h_0(x) & = (Hash(x) + 0^0)\ \%\ \ HashTableSize \\ If\ h_1(x) & = (Hash(x) + 1^1)\ \%\ \ HashTableSize \\ If\ h_2(x) & = (Hash(x) + 2^2)\ \%\ \ HashTableSize \\ & ... and\ so\ on\ if\ h_i\ is\ already\ full... \end{align}\end{split}\]
Example
\[h : \{50, 700, 76, 85, 92, 73, 101\}\]
\[\begin{split}\begin{align} h_0(50) &= 50\ \ \ \ \% \ 7 = 1 \\ h_0(700) & = 700\ \ \%\ 7 = 0 \\ h_0(76) &= 76\ \ \%\ 7 = 6 \\ h_0(85) &= 85\ \ \%\ 7 = 1 \\ & \Rightarrow h_1(85) = 85+(1*1)\ \ \%\ 7 = 2 \\ h_0(92) & f= 92\ \ \%\ 7 = 1 \\ & \Rightarrow h_1(92) = 92+(1*1)\ \ \%\ 7 = 2 \\ & \Rightarrow h_2(92) = 92+(2*2)\ \ \%\ 7 = 5 \\ h_0(73) &= 73\ \ \%\ 7 = 3 \\ h_0(101) &= 101\ \ \%\ 7 = 3 \\ & \Rightarrow h_1(101) = 101+(1*1)\ \ \%\ 7 = 4 \\ \end{align}\end{split}\]

Double Hashing#

Rule

\[\begin{split}\begin{align} H_{a}(x) &= Hash1(x)\ \%\ \ HashTableSize \\ H_{b}(x) &= Hash2(x)\ \%\ \ HashTableSize \\ \\ h(k, i) &= \bigg[h_{a}(k) + i * h_{b}(k) \bigg] \ \% \ n \\ \end{align}\end{split}\]

Example

\[h : \{50, 700, 76, 85, 92, 73, 101\}\]
\[size : 7\]
\[\begin{split}\begin{align} h_0(50) &= 50\ \ \ \ \% \ 7 = 1 \\ \\ h_0(700) & = 700\ \ \%\ 7 = 0 \\ \\ h_0(76) &= 76\ \ \%\ 7 = 6 \\ \\ \end{align}\end{split}\]

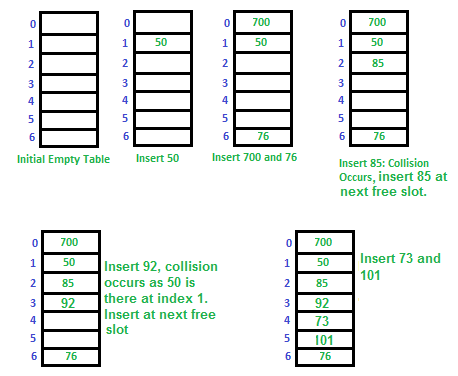
\(Arr[0]\)

\(700\)

\(Arr[1]\)

\(50\)

\(Arr[2]\)

\(Arr[3]\)

\(Arr[4]\)

\(Arr[5]\)

\(Arr[6]\)

\(76\)
\[\begin{split}\begin{align} h_0(85) &= 85\ \ \%\ 7 = 1 \\ h_1(85) &= \bigg[ h_{a}(85) + i * h_{b}(85) \bigg] \ \% \ 7 \\ &= \bigg[1 + 1 * (85\ \% \ 7) \bigg] \ \% \ 7 \\ &= \bigg[1 + 1 * 1 \bigg] \ \% \ 7 \\ &= 2 \\ \end{align}\end{split}\]

\(Arr[0]\)

\(700\)

\(Arr[1]\)

\(50\)

\(Arr[2]\)

\(85\)

\(Arr[3]\)

\(Arr[4]\)

\(Arr[5]\)

\(Arr[6]\)

\(76\)
\[\begin{split}\begin{align} h_0(92) &= 92\ \ \%\ 7 = 1 \\ h_1(92) &= \bigg[ h_{a}(92) + i * h_{b}(92) \bigg] \ \% \ 7 \\ &= \bigg[1 + 1 * (92\ \% \ 7) \bigg] \ \% \ 7 \\ &= \bigg[1 + 1 * 1 \bigg] \ \% \ 7 \\ &= 2 \\ h_2(92) &= \bigg[ h_{a}(92) + i * h_{b}(92) \bigg] \ \% \ 7 \\ &= \bigg[1 + 2 * (92\ \% \ 7) \bigg] \ \% \ 7 \\ &= \bigg[1 + 2 * 1 \bigg] \ \% \ 7 \\ &= 3 \\ \end{align}\end{split}\]

\(Arr[0]\)

\(700\)

\(Arr[1]\)

\(50\)

\(Arr[2]\)

\(85\)

\(Arr[3]\)

\(92\)

\(Arr[4]\)

\(Arr[5]\)

\(Arr[6]\)

\(76\)
\[\begin{split}\begin{align} h_0(73) &= 73\ \ \% \ 7 = 3 \\ h_1(73) &= \bigg[ h_{a}(73) + i * h_{b}(73) \bigg] \ \% \ 7 \\ &= \bigg[3 + 1 * (73\ \% \ 7) \bigg] \ \% \ 7 \\ &= \bigg[3 + 1 * 3 \bigg] \ \% \ 7 \\ &= 6 \\ h_2(73) &= \bigg[ h_{a}(73) + i * h_{b}(73) \bigg] \ \% \ 7 \\ &= \bigg[3 + 2 * (73\ \% \ 7) \bigg] \ \% \ 7 \\ &= \bigg[3 + 2 * 3 \bigg] \ \% \ 7 \\ &= 2 \\ h_3(73) &= \bigg[ h_{a}(73) + i * h_{b}(73) \bigg] \ \% \ 7 \\ &= \bigg[3 + 3 * (73\ \% \ 7) \bigg] \ \% \ 7 \\ &= \bigg[3 + 3 * 3 \bigg] \ \% \ 7 \\ &= 5 \\ \end{align}\end{split}\]

\(Arr[0]\)

\(700\)

\(Arr[1]\)

\(50\)

\(Arr[2]\)

\(85\)

\(Arr[3]\)

\(92\)

\(Arr[4]\)

\(Arr[5]\)

\(73\)

\(Arr[6]\)

\(76\)
\[\begin{split}\begin{align} h_0(101) &= 101\ \ \%\ 7 = 3 \\ h_1(101) &= \bigg[ h_{a}(101) + i * h_{b}(101) \bigg] \ \% \ 7 \\ &= \bigg[3 + 1 * (101\ \% \ 7) \bigg] \ \% \ 7 \\ &= \bigg[3 + 1 * 3 \bigg] \ \% \ 7 \\ &= 6 \\ h_2(101) &= \bigg[ h_{a}(101) + i * h_{b}(101) \bigg] \ \% \ 7 \\ &= \bigg[3 + 2 * (101\ \% \ 7) \bigg] \ \% \ 7 \\ &= \bigg[3 + 2 * 3 \bigg] \ \% \ 7 \\ &= 2 \\ h_3(101) &= \bigg[ h_{a}(101) + i * h_{b}(101) \bigg] \ \% \ 7 \\ &= \bigg[3 + 3 * (101\ \% \ 7) \bigg] \ \% \ 7 \\ &= \bigg[3 + 3 * 3 \bigg] \ \% \ 7 \\ &= 5 \\ h_4(101) &= \bigg[ h_{a}(101) + i * h_{b}(101) \bigg] \ \% \ 7 \\ &= \bigg[3 + 4 * (101\ \% \ 7) \bigg] \ \% \ 7 \\ &= \bigg[3 + 4 * 3 \bigg] \ \% \ 7 \\ &= 1 \\ h_5(101) &= \bigg[ h_{a}(101) + i * h_{b}(101) \bigg] \ \% \ 7 \\ &= \bigg[3 + 5 * (101\ \% \ 7) \bigg] \ \% \ 7 \\ &= \bigg[3 + 5 * 3 \bigg] \ \% \ 7 \\ &= 4 \\ \end{align}\end{split}\]

\(Arr[0]\)

\(700\)

\(Arr[1]\)

\(50\)

\(Arr[2]\)

\(85\)

\(Arr[3]\)

\(92\)

\(Arr[4]\)

\(101\)

\(Arr[5]\)

\(73\)

\(Arr[6]\)

\(76\)

Comparison#

Linear Probing

  • Easy to implement

  • Best cache performance

  • Suffers from clustering

Quadratic Probing

  • Average cache performance

  • Suffers less from clustering

Double Hashing

  • Poor cache performance

  • No clustering

  • Requires more computation time