Graphs

TL;DR

A graph is a data structure that consists of a set of vertices (also known as nodes) and a set of edges connecting them. The edges represent the relationships or connections between the vertices, and can be directed (pointing from one vertex to another) or undirected (connecting two vertices in both directions).

Graphs can be used to represent a wide range of real-world systems and networks, such as social networks, transportation networks, and computer networks. They are an important tool in computer science and are used in many applications, such as data mining, machine learning, and optimization.

Graphs can be represented in different ways, such as adjacency lists, adjacency matrices, and edge lists. Adjacency lists are a common representation, where each vertex is associated with a list of its adjacent vertices (i.e., the vertices that it is directly connected to).

Graph algorithms are used to analyze and manipulate graphs. Some common graph algorithms include traversal algorithms (such as depth-first search and breadth-first search), shortest path algorithms (such as Dijkstra’s algorithm and the Bellman-Ford algorithm), and minimum spanning tree algorithms (such as Kruskal’s algorithm and Prim’s algorithm).

Overall, graphs are an important data structure in computer science, and understanding them is essential for solving many problems in fields such as computer networking, social network analysis, and transportation planning.

Additional Resources

Graph

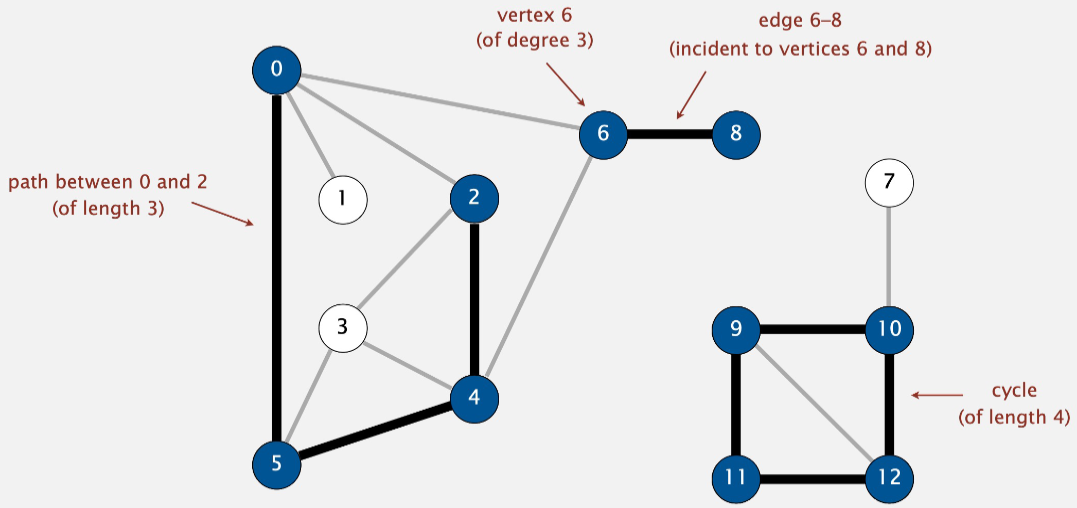
• a set of vertices connect pairwise by edges

Vertices

• fundamental units of the graph known as vertex or nodes;

• every node/vertex can be labeled or unlabelled

Edges

• are drawn or used to connect two nodes of the graph

• can connect any two nodes in any possible way

• can be labeled or unlabelled

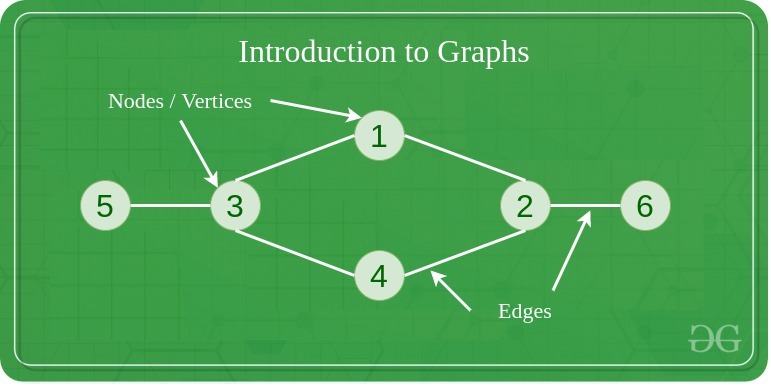
Fig. 70 gfg: graph vertices and edges

Examples

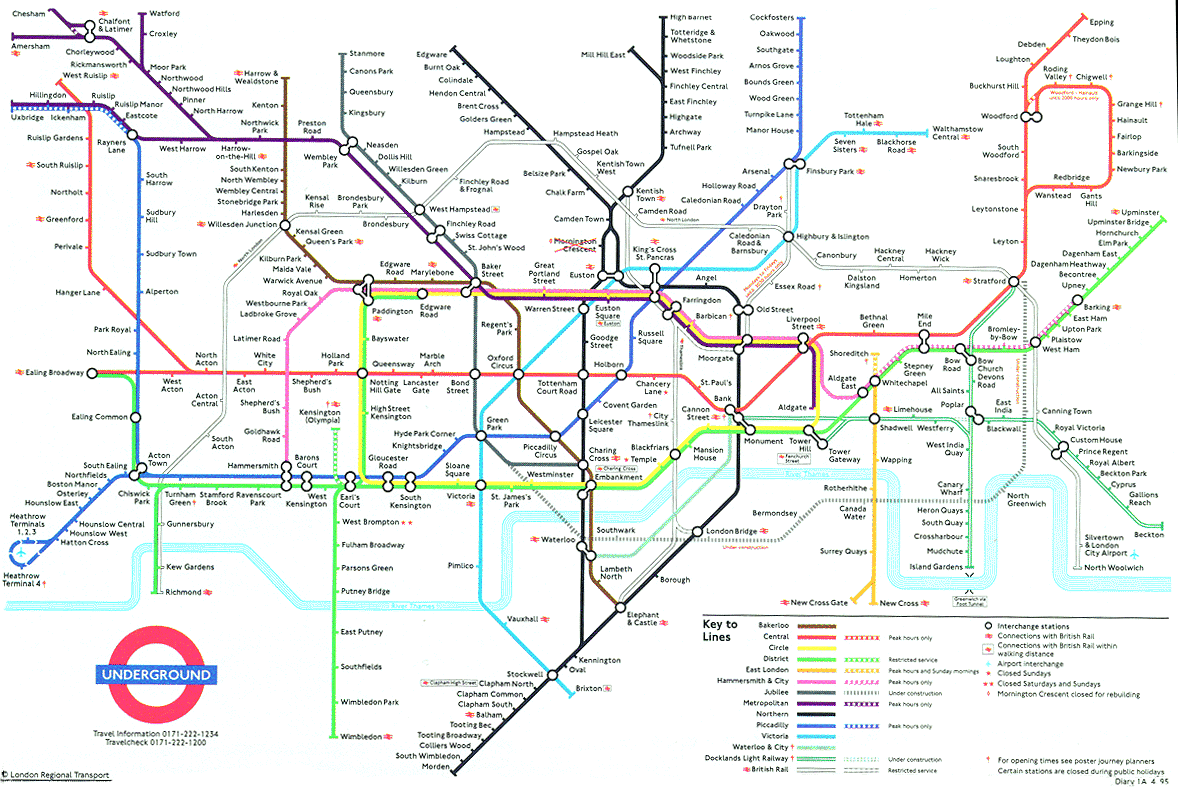
Fig. 71 London Underground (Tube) Map
vertex = subway stop;
edge = direct route

Fig. 72 Facebook Social Network Map:
vertex = person;
edge = social relationship

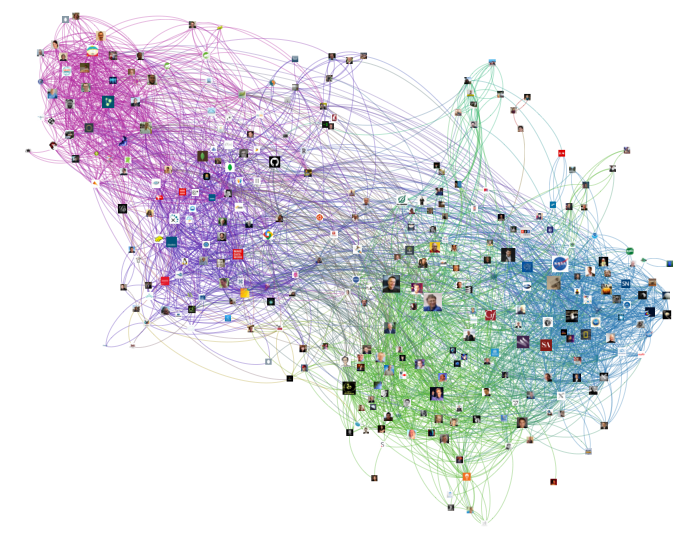
Fig. 73 Twitter followers
vertex = Twitter account;
edge = Twitter follower

Fig. 74 Protein-protein interation network
vertex = protein;
edge = interaction

Applications

graph	vertex	edge
cell phone	phone	placed call
infectious disease	person	infection
financial	stock, currency	transactions
transportation	intersection	street
internet	router	fiber cable
web	web page	URL link
social relationship	person	friendship

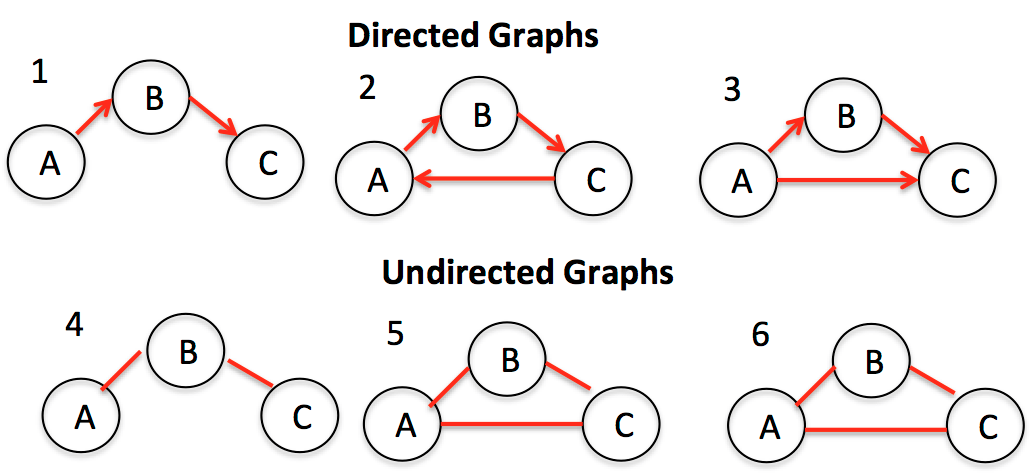
Graph Types

Types

Undirected

Graph

a set of vertices connect pairwise by edges

Path

sequence of vertices connected by edges, with no repeated edges

Definition

two vertices are connected if there is a path between them

Cycle

path (with \(\ge 1\) edge) whose first and last vertices are the same

Directed

Graph

a set of vertices connect pairwise by edges

Directed Path

sequence of vertices connected by edges, with no repeated edges

Definition

vertex \(w\) is reachable from vertex \(v\) if there is a directed path from \(v\) to \(w\)

Directed Cycle

directed path (with \(\ge 1\) edge) whose first and last vertices are the same

Graph Processing Problems

problem	description
s-t path	Find a path between \(s\) and \(t\)
shortest s-t path	Find a path with the fewest edges between \(s\) and \(t\)
cycle	Find a cycle
Euler cycle	Find a cycle that uses each edge exactly once
Hamilton cycle	Find a cycle that uses each vertex exactly once
connectivity	Is there a path between ev ery pair of vertices?
graph isomorphism	Are two graphs isomorphic?
planarity	Draw the graph in the plane with no crossing edges

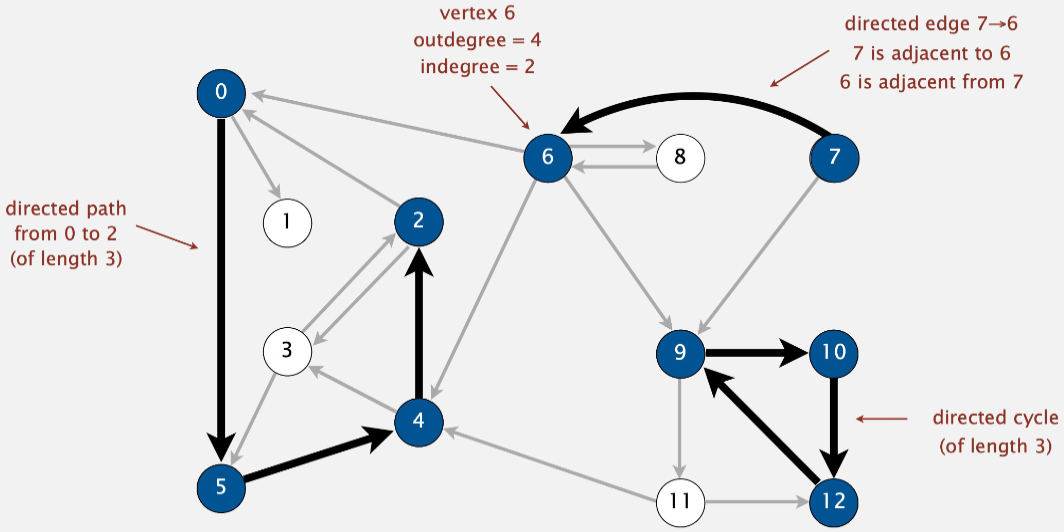
Representation

Digraph

Vertex representation

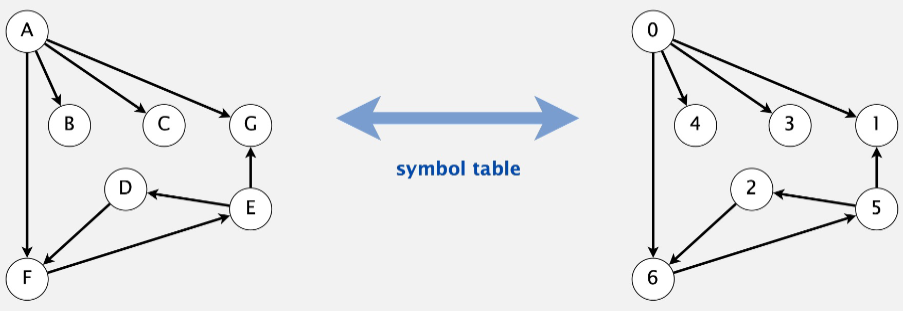
For 0 through all positive values \(V-1\) Applications: use symbol table to convert between names and integers

Definition

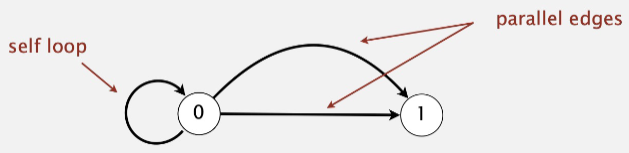
a digraph is simple if it has no self-loops or parallel edges

Adjacency-matrix

Maintain a \(V-by-V\) boolean array;

For each edge \(v \rightarrow w\) in the digraph

\[adj[v][w] \ =\ true\]

Adjacency-lists

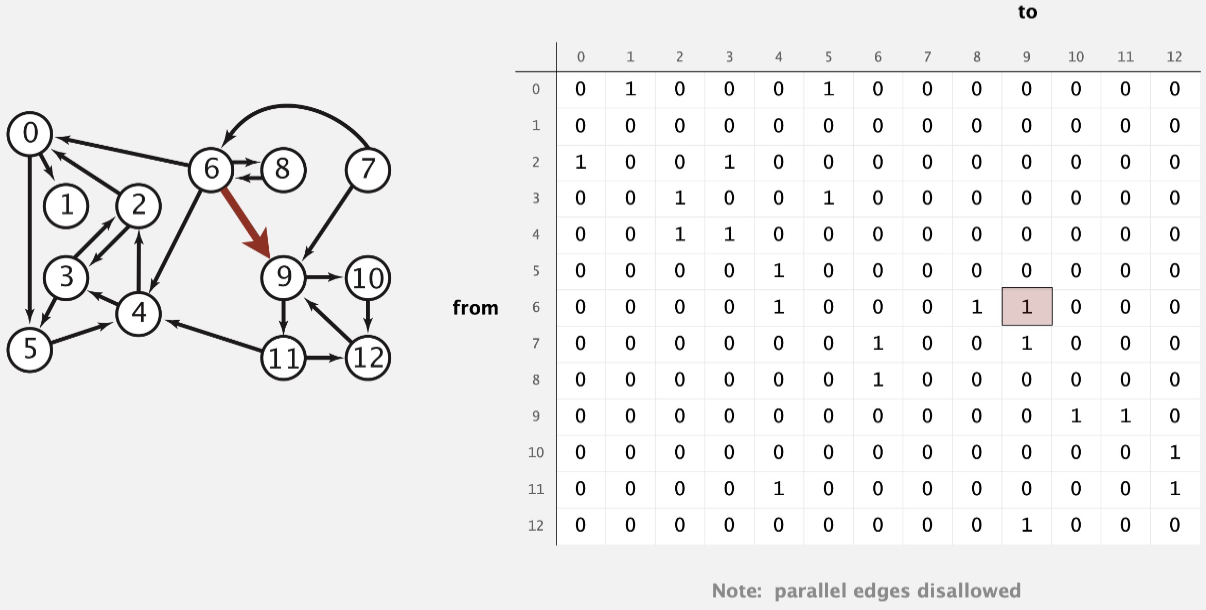
Maintain vertex-indexed array of lists

In practice

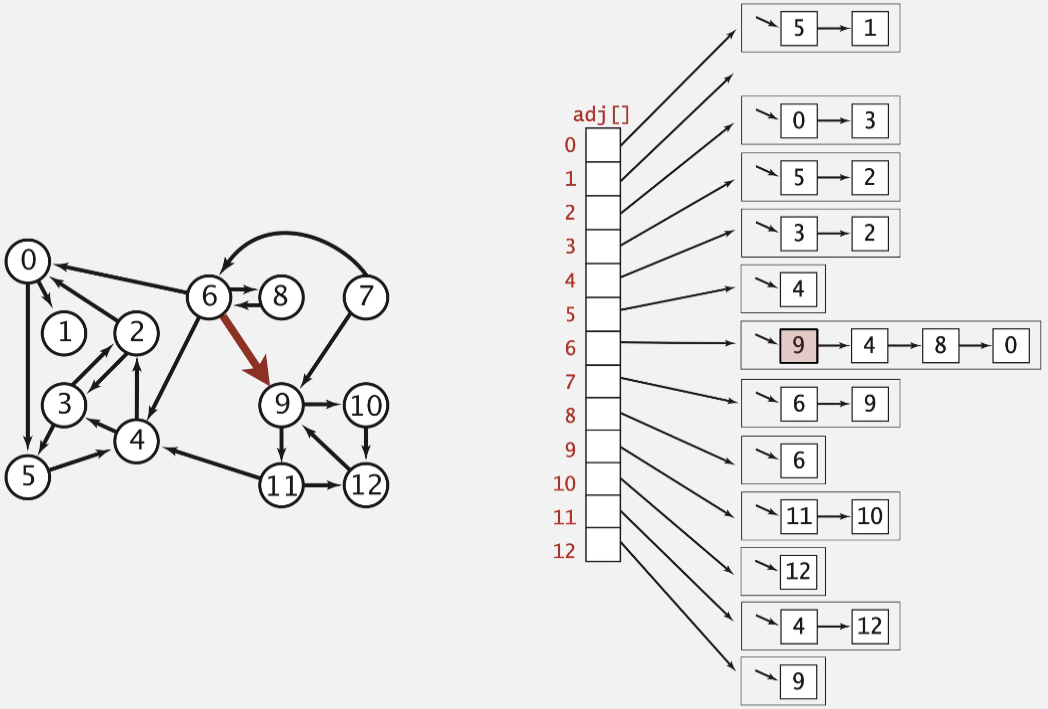
Use adjacency-lists

Algorithms based on iterating over vertices adjacent from \(v\)
Real-world graphs tend to be sparce (\(\Theta(V)\) edges), not dense (\(\Theta(V^2)\) edges)

representation	space	add edge from \(v\) to \(w\)	has edge from \(v\) to \(w\)	iterate over vertices adjacent from \(v\)?
adjacent matrix	\(V^2\)	1*	1	\(V\)
adjacent lists	\(E+V\)	1	\(outdegree(v)\)	\(outdegree(v)\)

* disallows parallel edges