Search Algorithms

TL;DR

Search algorithms are a fundamental concept in data structures and algorithms that are used to find an item in a collection of data. There are several types of search algorithms, each with its own strengths and weaknesses.

Linear search is a simple search algorithm that examines each element in a collection until the desired item is found. Linear search is easy to implement and works well for small collections or unsorted data, but it can be inefficient for large collections or when the desired item is near the end of the collection.

Binary search is a more efficient search algorithm that works on sorted collections. Binary search divides the collection in half at each step and eliminates one half of the remaining items based on the comparison with the target value. Binary search has a time complexity of \(O(log\ n)\), making it much faster than linear search for large collections.

Hashing is another search algorithm that works by using a hash function to map the search key to an index in an array. Hashing provides fast access to items with a time complexity of \(O(1)\), but it requires a good hash function and can suffer from collisions where multiple items map to the same index.

Tree-based search algorithms, such as binary search trees and balanced trees, provide efficient search operations with time complexity of \(O(log\ n)\). They are particularly useful for data that needs to be sorted, and can also be used for other operations such as insertion, deletion, and traversal.

The choice of search algorithm depends on the properties of the data and the specific requirements of the application. By choosing the most appropriate search algorithm, programmers can improve the efficiency and effectiveness of their programs.

Additional Resources

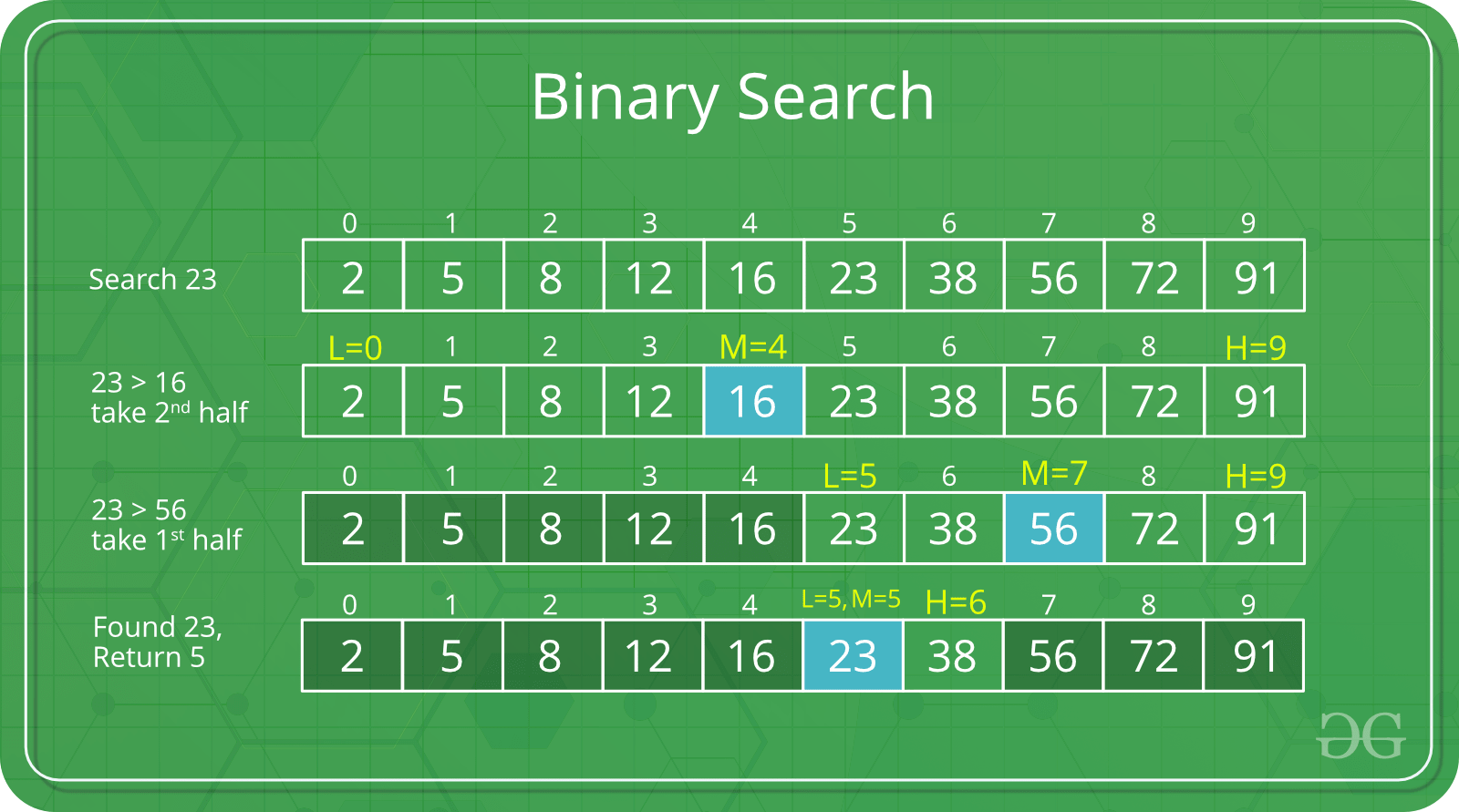
Binary Search

• repeatedly target the center of the search structure and divide the search space in half.

• ex. binary search

• note: specifically designed for searching in sorted data-structures…

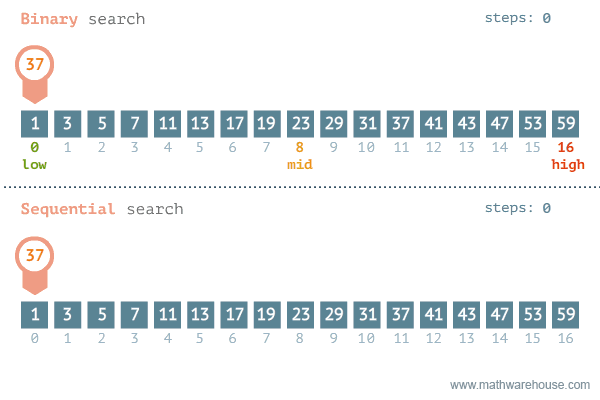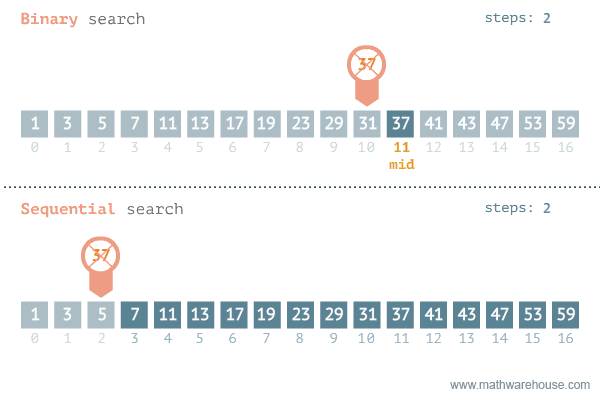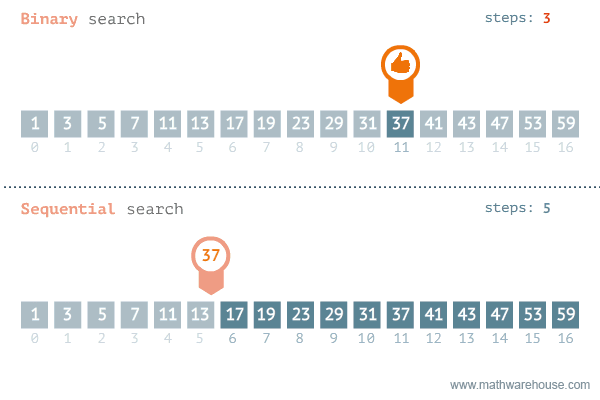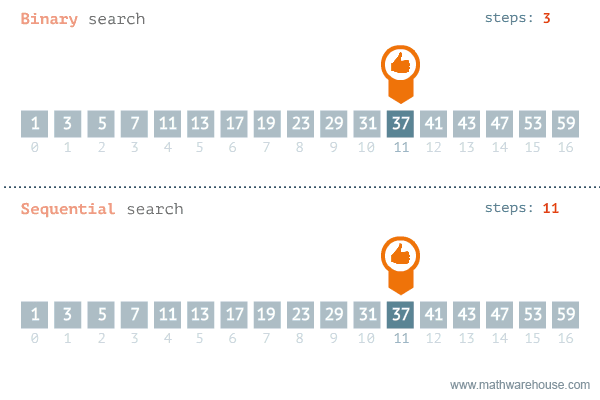
Sequential Search

• the list or array is traversed sequentially and every element is checked.

• ex. linear search

Linear Search

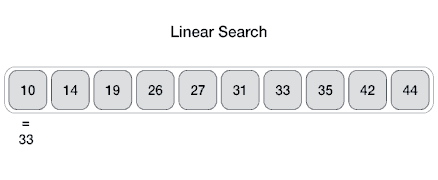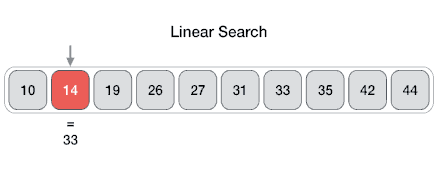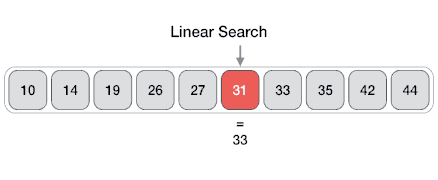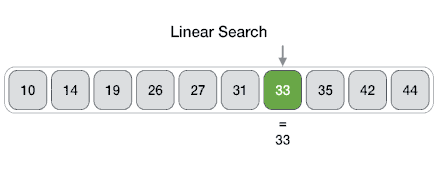
https://www.tutorialspoint.com/data_structures_algorithms/images/linear_search.gif

Linear Search: Implementation

// Pseudocode
// -
// Iterate from 0 to N-1, 
// compare the value of every index with x 
// if they match, return index
### <b>

int linearSearch(int array[], int n, int x) {      
    // Going through array sequencially
    for (int i = 0; i < n; i++)
        if (array[i] == x) return i;
    return -1;
}

Linear Search: Implementation

Rules

• Consider all possible cases.

• Find the number of comparisons for each case.

• Add the number of comparisons and divide by the number of cases.

Best-case \( \Rightarrow T(n) = O(1)\)

\[target = A_0 = 1\ comparison\]

Worst-case \( \Rightarrow T(n) = O(n)\)

\[target = A_{n - 1} = n\ comparisons\]

Average-case (in a successful search) \( \Rightarrow T(n) = O(n)\)

\[\frac{1 + 2 + ... + n}{n} = \frac{1}{n}*\frac{n(n + 1)}{2} = \frac{n + 1}{n}\]

Binary Search

Pseudocode

Approaches

Iterative Approach

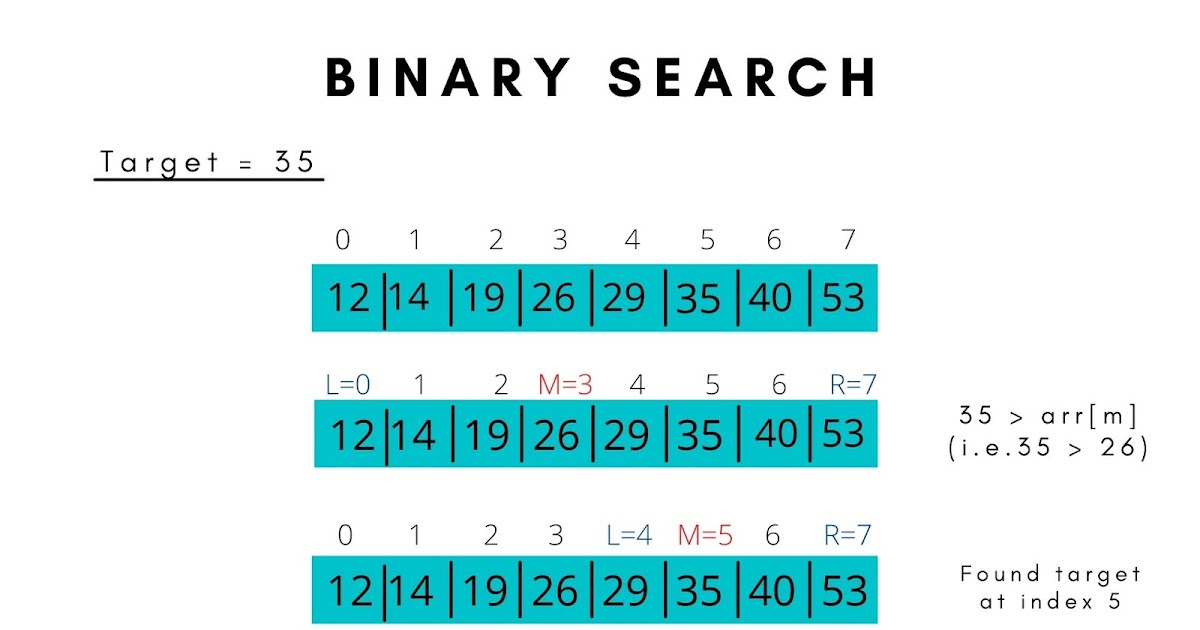
• Consider start index to be at \(0\) and last index to be n-1 index at starting

  • \(n \rightarrow length\)

• Find middle index mid of the array

• If key is found to be less than mid index element then update last index of the array to mid - 1

• Else if key is found to be greater than mid index element then update start index of the array to mid + 1

• Else check for mid index element with key if not match repeat the above steps til start index is less than end index

Recursive Approach

• If start is less than end perform Binary search else terminate the algorithm.

• If the element at mid (middle index) is equal to the key then return the index as it found the key

• Else if the key is less than mid (the element middle index) then call the function by passing end as mid - 1 (as key will be less than mid element)

• Else if the key is greater than mid then call the function by passing start as mid + 1 (as key will be greater than mid)

https://www.geeksforgeeks.org/linear-search-vs-binary-search/?ref=rp

https://takeuforward.org/data-structure/binary-search-explained/

Binary Search

iterative

int binarySearch(int array[], int x, int low, int high) {
    // Repeat until the pointers low and high meet each other
    while (low <= high) {
        int mid = low + (high - low) / 2;
        if (array[mid] == x) return mid;
        if (array[mid] < x) low = mid + 1;
        else high = mid - 1;
    }
    return -1;
}

Binary Search: Iterative

visualize: iterative

recursive

int binarySearch(int arr[], int start, int end, int k) {
  if (start > end) return -1;
  int mid = (start + end) / 2;
  if (k == arr[mid]) return mid;
  else if (k < arr[mid]) return binarySearch(arr, start, mid - 1, k);
  else return binarySearch(arr, mid + 1, end, k);
}

Binary Search: Recursive

visualize: recursive

Analysis

Rules

• Break down the problem into sub-problems

• Solve the sub problems

• Merge the sub problems to get desired Output

• Note: Must be sorted

Best-case \( \Rightarrow T(n) = O(1)\)

\[target\ is\ first\ comparison\]

Worst-case \( \Rightarrow T(n) = O(log\ n)\)

\[target\ is\ last\ comparison\]

Average-case (in a successful search) \( \Rightarrow T(n) = O(log\ n)\)

\[target\ is\ neither first\ nor\ last\ comparison\]

Linear v. Binary

Linear	Binary
Input data need not to be in sorted.	Input data need to be in sorted order.
Also called sequential search.	Also called half-interval search.
\(T(n) = O(n)\)	\(T(n) = O(log\ n)\)
Multidimensional array can be used	Only single dimensional array is used
Performs equality comparisons	Performs ordering comparisons
Less complex.	More complex.
Very slow process.	Very fast process.