Recursive Algorithms (Analysis)#
TL;DR

A recursive algorithm is an algorithm that calls itself to solve a problem. It is a powerful technique used in computer science to solve complex problems by breaking them down into smaller sub-problems.
The analysis of recursive algorithms involves determining the number of times the algorithm will call itself and the amount of work that is done at each level of recursion. This analysis is important because it helps us understand the efficiency of the algorithm and how it scales with input size.
The time complexity of a recursive algorithm is often expressed in terms of a recurrence relation, which describes the relationship between the time taken by the algorithm at each level of recursion. Solving the recurrence relation allows us to determine the overall time complexity of the algorithm.
Recursive algorithms are commonly used in data structures and algorithms, such as sorting, searching, and graph traversal. For example, the quicksort algorithm is a well-known sorting algorithm that uses recursion to divide a large array into smaller sub-arrays.
While recursive algorithms can be elegant and powerful, they can also be inefficient if not carefully designed. Recursive algorithms can lead to stack overflow if the depth of the recursion becomes too large, which can happen if the input size is large or if the recursion is not properly bounded. Therefore, careful analysis and design are necessary when using recursive algorithms.
Iteration v. Recursion#
Iterative
1#include <iostream>
2
3int factorialIterative(int n) {
4 int result = 1;
5 for (int i = 1; i <= n; ++i) {
6 result *= i;
7 }
8 return result;
9}
10
11int main() {
12 int num = 5;
13 int result = factorialIterative(num);
14 std::cout << "Factorial of " << num << " is: " << result << std::endl;
15 return 0;
16}
The iterative function factorialIterative calculates the factorial by using a loop. It initializes result to 1 and then iterates over the numbers from 1 to n, multiplying each number with the current value of result to accumulate the factorial.
Recursive
1#include <iostream>
2
3int factorialRecursive(int n) {
4 if (n == 0)
5 return 1;
6 else
7 return n * factorialRecursive(n - 1);
8}
9
10int main() {
11 int num = 5;
12 int result = factorialRecursive(num);
13 std::cout << "Factorial of " << num << " is: " << result << std::endl;
14 return 0;
15}
The recursive function factorialRecursive calculates the factorial by breaking down the problem into smaller sub-problems. The base case is when n equals 0, and for any other value of n, the factorial is computed by multiplying n with the factorial of n-1.
Recursion#

The process of solving a problem by reducing it to smaller versions of itself
Solve a task by reducing it to smaller tasks (of the same structure)
Technically, a recursive function is one that calls itself
1int someFunction() {
2 if (base_case) {
3 // calculate trivialSolution
4 } else {
5 // break task into subtasks
6 // solve each task recursively
7 // merge solutions if necessary
8 }
9}
base case
solution for a trivial case
it can be used to stop the recursion (prevents “stack overflow”)
every recursive algorithm needs at least one base case
recursive calls
divide problem into smaller instance(s) of the same structure
Every recursive definition must have one (or more) base cases.
The general case must eventually be reduced to a base case.
The base case stops the recursion.
Can we live without it?
yes, you can write “any program” with arrays, loops, and conditionals
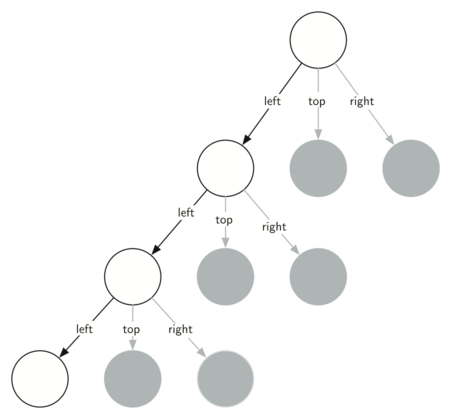
Fig. 94 https://courses.cs.washington.edu/courses/cse120/17sp/labs/11/tree.html#
Caveats?
The choice between a recursive algorithm and an iterative algorithm depends on several factors. Here are some scenarios where a recursive algorithm may be more suitable:
- Problems with inherent recursive structure
Recursive algorithms are well-suited for solving problems that have a natural recursive structure. If the problem can be easily divided into smaller sub-problems that are of the same type as the original problem, a recursive solution can be intuitive and concise.
- Problems involving backtracking or tree/graph traversal
Recursive algorithms are commonly used in backtracking scenarios, where you explore different paths or combinations to find a solution. Similarly, tree or graph traversal problems, such as depth-first search or recursive tree traversals, often lend themselves well to recursive solutions.
- Problems with smaller problem sizes
Recursive algorithms can be more efficient when dealing with smaller problem sizes. If the problem size is relatively small, the overhead of recursive function calls may not significantly impact performance.
- Problems with divide-and-conquer approach
Recursive algorithms are often employed in divide-and-conquer strategies. If the problem can be divided into independent sub-problems that can be solved individually and then combined to obtain the final result, a recursive approach can be beneficial.
Considerations?
Recursive algorithms may have some drawbacks, such as increased memory usage due to the recursive function call stack, potential performance issues for large problem sizes, and the possibility of exceeding the stack size limit in certain programming languages.
Iterative algorithms can be advantageous in scenarios where a loop structure and mutable variables can be used to iteratively solve the problem without incurring the overhead of recursive function calls.
Ultimately, the choice between recursive and iterative algorithms depends on the nature of the problem, the problem size, the available resources, and the trade-offs between simplicity, efficiency, and readability of the code.
Recursive Call Tree#
To find the largest element in list[a]…list[b]
a. Find the largest element in list[a + 1]...list[b] and call it max
b. Compare the elements list[a] and max
if (list[a] >= max)the largest element inlist[a]...list[b]islist[a]otherwise, the largest element in
list[a]...list[b]ismax
1int largest (const int list[], int lowerIndex, int upperIndex) {
2 int max;
3 if (lowerIndex == upperIndex) //size of the sublist is one
4 return list[lowerIndex];
5 else {
6 max = largest(list, lowerIndex + 1, upperIndex);
7 if (list[lowerIndex] >= max)
8 return list[lowerIndex];
9 else
10 return max;
11 }
12}
1int sum_array(int *A, int n) {
2 //basecase
3 if (n == 1)
4 return A[0];
5
6 //solve sub-task
7 int sum = sum_array(A, n - 1);
8
9 //return
10 return A[n - 1] + sum;
11}
Visualize
May take a moment to load…
1void drawSierpinski(int n, int x, int y) {
2 if (n == 0) {
3 std::cout << "Drawing triangle at (" << x << ", " << y << ")" << std::endl;
4 } else {
5 int sideLength = pow(2, n - 1); // Length of each side of the triangle
6 int height = sideLength * sqrt(3) / 2; // Height of the equilateral triangle
7
8 drawSierpinski(n - 1, x, y);
9 drawSierpinski(n - 1, x + sideLength / 2, y);
10 drawSierpinski(n - 1, x + sideLength / 4, y + height / 2);
11 }
12}
1int bsearch(int *A, int lo, int hi, int k) {
2 //base case
3 if (hi < lo)
4 return NOT_FOUND;
5
6 // calculate mid point index
7 int mid = lo + ( (hi - lo) / 2);
8 // key found?
9 if (A[mid] == k)
10 return mid;
11 // key in upper subarray?
12 if (A[mid] < k)
13 return bsearch(A, mid + 1, hi, k);
14 // key is in lower subarray?
15 return bsearch(A, lo, mid - 1, k);
16}
https://www.cs.usfca.edu/~galles/visualization/Search.html
Unimodal Arrays#
Define
An array is (strongly) unimodal if it can be split into an increasing part followed by a decreasing part
An array is (weakly) unimodal if it can be split into a non-decreasing part followed by a non-increasing part
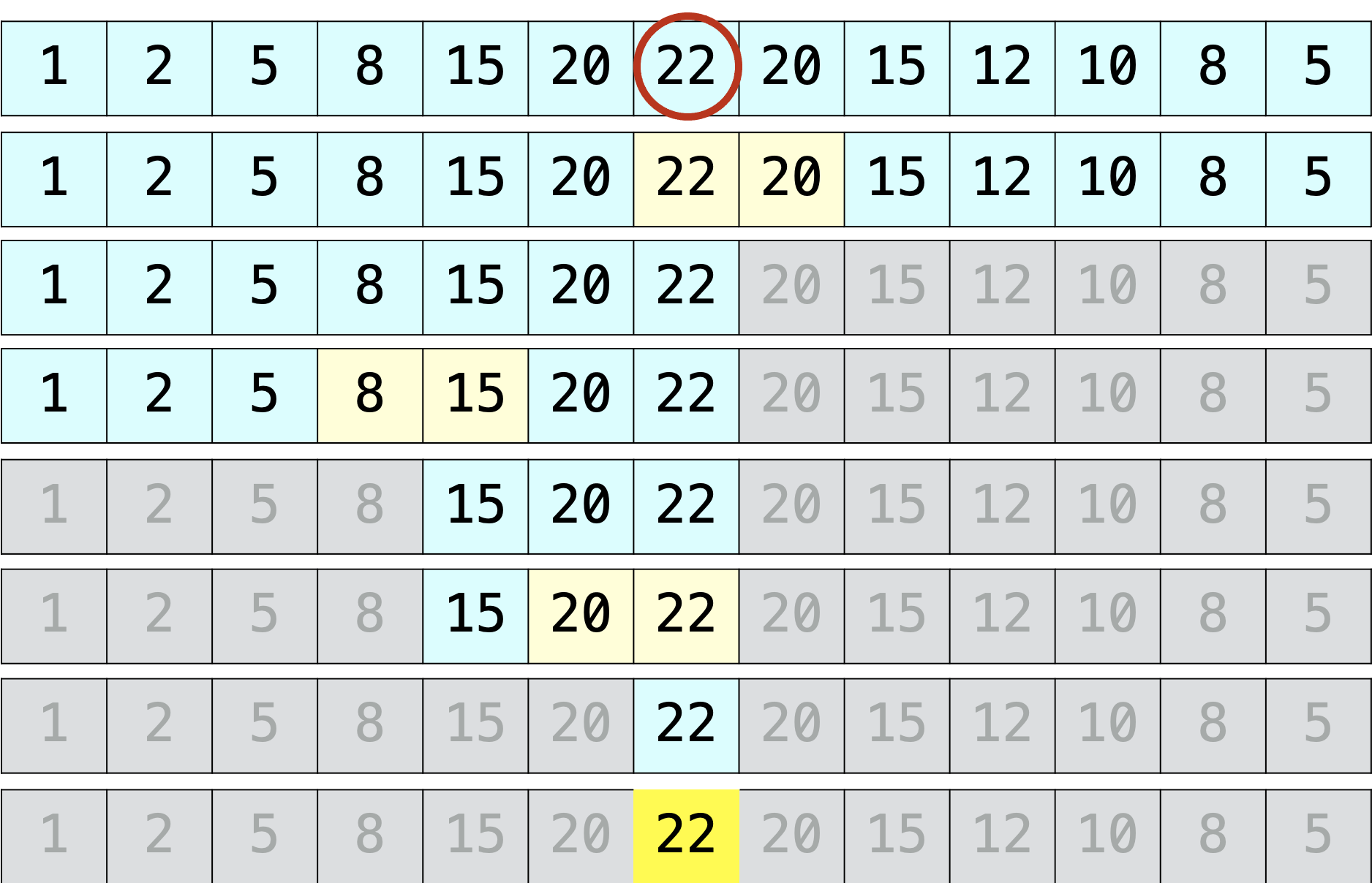
Find the max (strongly unimodal)#
No Skew

1int max_s_unimodal (int *A, int low, int hi) {
2 if (low == hi)
3 return A[low];
4
5 int mid = (low + hi) / 2;
6
7 if (A[mid] < A[mid+1])
8 return max_s_unimodal(A, mid + 1, hi);
9 else
10 return max_s_unimodal(A, low, mid);
11}
Visualize
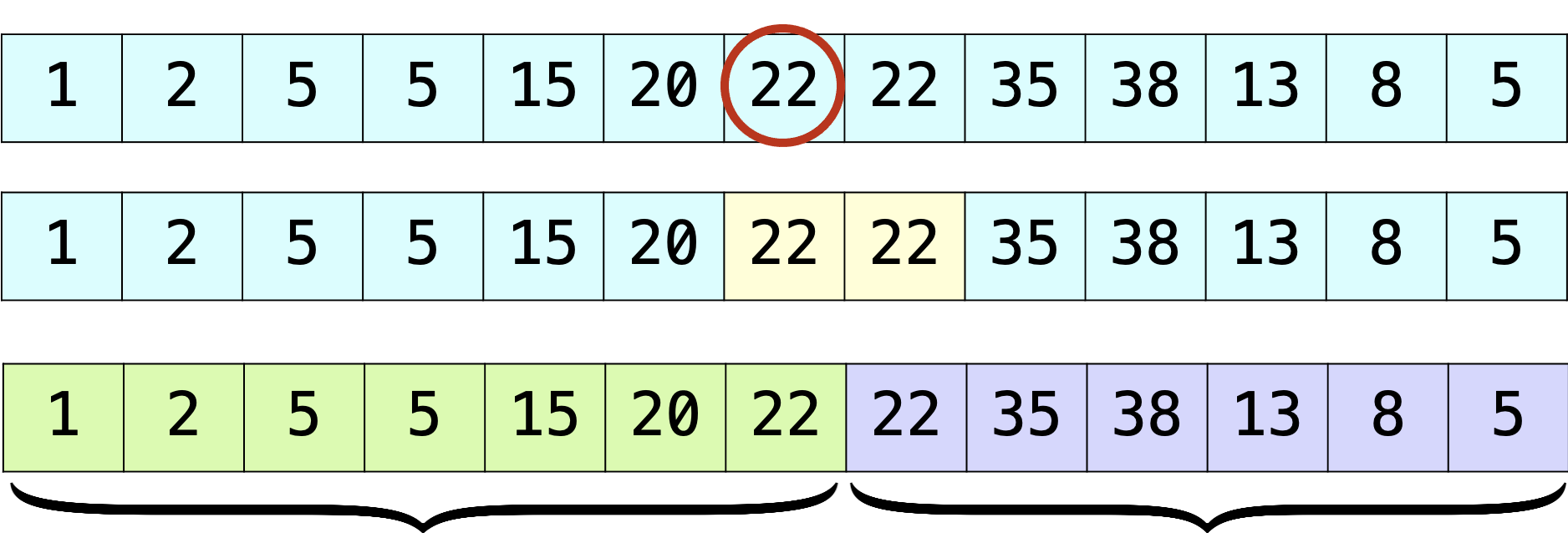
Find the max (weakly unimodal)#
1int max_w_unimodal (int *A, int low, int hi) {
2 if (low == hi)
3 return A[low];
4
5 int mid = (low + hi) / 2;
6
7 if (A[mid] < A[mid + 1])
8 return max_w_unimodal(A, mid + 1, hi);
9 else if (A[mid] > A[mid + 1])
10 return max_w_unimodal(A, low, mid);
11 else {
12 int left = max_w_unimodal(A, mid+1, hi);
13 int right = max_w_unimodal(A, low, mid);
14 return std::max(left, right);
15 }
16}
Visualize
Bimodal Arrays#
1int bimodalMax(int array[], int start, int end) {
2 if (start == end) {
3 return array[start]; // Base case: Only one element
4 }
5 int mid = (start + end) / 2;
6 int leftMax = bimodalMax(array, start, mid); // Maximum in the left sub-array
7 int rightMax = bimodalMax(array, mid + 1, end); // Maximum in the right sub-array
8
9 return max(leftMax, rightMax); // Compare and return the maximum of leftMax and rightMax
10}
Comparison & Other Modalities#