Recurrences#
Recurrence relations are mathematical expressions that define the runtime of algorithms or the space complexity of data structures recursively in terms of their input size. In other words, they describe the time or space complexity of an algorithm by expressing it as a function of the size of the input data.
In the context of data structures and algorithms, recurrences are commonly used to analyze the performance of recursive algorithms such as quicksort, mergesort, and binary search. By using recurrence relations, we can obtain a closed-form expression for the runtime complexity of such algorithms and make predictions about their performance as the input size grows.
Solving recurrence relations can be challenging, and there are several methods to do so, including the substitution method, the recursion tree method, and the master theorem. Understanding and using recurrence relations is an important skill for anyone studying data structures and algorithms, as it enables them to analyze the performance of algorithms and design more efficient solutions.
Factorial of n (formula)#
For each positive integer \(n\), the quantity \(n\) factorial denoted \(n!\), is defined to be the product of all the integers from \(1\) to \(n\):
\[n! = n · (n − 1) \dots 3·2·1\]Zero factorial, denoted 0!, is defined to be 1:
\[0! = 1\]– Discrete Mathematics with Applications, 4th
Simplify the following expressions:
\(\frac{8!}{7!}\)
\(\frac{5!}{2!*3!}\)
\(\frac{(n)!}{(n - 3)!}\)
code
1int fact(int num) {
2
3 if (num == 0) return 1;
4
5 else return num * fact(num - 1);
6}
Permutation
gives the number of ways to select \(r\) elements from \(n\) elements when order matters
Three different fruits are to be distributed among a group of 10 people. Find the total number of ways this can be possible.
\(n = 10,\ r = 3 \dots =\ ^{10}P_3\)
Combination
gives the number of ways to select \(r\) elements from \(n\) elements where order does not matter
Find the number of ways 3 students can be selected from a class of 50 students.
\(n = 50,\ r = 3 \dots =\ ^{50}C_3\)
Recurrence Relations#
By itself, a recurrence does not describe the running time of an algorithm
need a closed-form solution (non-recursive description)
exact closed-form solution may not exist, or may be too difficult to find
For most recurrences, an asymptotic solution of the form \(\Theta()\) is acceptable
…in the context of analysis of algorithms
Methods of Solving Recurrences#
In the unrolling method, we repeatedly substitute the recurrence relation into itself until we reach a base case. Let’s unroll the recurrence relation for a specific value of \(n\):
We continue this process until we reach the base case, which occurs when \(\frac{n}{2^k} = 1\). Solving for \(k\), we find that \(k = log_2\ (n)\). Therefore, the final unrolled expression becomes:
Since \(T(1)\) is a constant, we can simplify the expression further:
Thus, the solution obtained through unrolling suggests that the time complexity of the original recurrence relation is \(O(n\ log_2 (n))\).
In the guessing method, we make an educated guess or hypothesis about the form of the solution based on the recurrence relation. We then use mathematical induction or substitution to prove our guess.
Let’s guess that the solution to the recurrence relation \(T(n) = 2T(\frac{n}{2}) + n\) is \(T(n) = O(n\ log\ (n))\).
We assume that \(T(k) ≤ ck\ log\ (k)\) for some constant \(c\), where \(k < n\). Now we substitute this assumption into the recurrence relation:
To ensure that \(T(n) ≤ cn\ log\ (n)\) holds, we need to find a value of \(c\) such that \((n - cn) ≤ 0\). By choosing \(c ≥ 1\), we can guarantee that \(T(n) ≤ cn\ log\ (n)\).
Hence, the solution \(T(n) = O(n\ log\ (n))\) satisfies the recurrence relation.
In the recursion tree method, we draw a tree to represent the recursive calls made in the recurrence relation. Each level of the tree corresponds to a recursive call, and we analyze the work done at each level.
For our example, the recursion tree for \(T(n) = 2T(\frac{n}{2}) + n\) would have a root node representing \(T(n)\), two child nodes representing \(T(\frac{n}{2})\), and so on. Each node represents a recursive call, and the work done at each node is represented by the term n.
The recursion tree will have \(log_2\ (n)\) levels since we divide the problem size by \(2\) at each level. At each level, the work done is \(n\), and there are \(2^i\) nodes at level \(i\). Therefore, the total work at each level is \(2^i * n\).
Summing up the work done at each level, we have:
This is a geometric series with a common ratio of \(2\) and the first term being \(n\). The sum of this series is given by:
Therefore, the time complexity of the recurrence relation is \(O(n^2)\).
Note that in this example, the unrolling and guessing methods led to a time complexity of \(O(n\ log\ (n))\), while the recursion tree method resulted in \(O(n^2)\). The discrepancy arises because the recursion tree method accounts for the exact work done at each level, while the other methods provide upper bounds or estimations.
The master theorem is a mathematical formula used to analyze the time complexity of divide-and-conquer algorithms. It provides a solution for recurrence relations of the form:
Where:
\(T(n)\) represents the time complexity of the algorithm, \(a\) is the number of recursive subproblems, \(\frac{n}{b}\) is the size of each subproblem, \(f(n)\) is the time complexity of the remaining work done outside the recursive calls.
The master theorem provides three cases based on the relationship between \(f(n)\) and the subproblem part \(aT(\frac{n}{b})\).
- Case 1
If \(f(n) = O(n^c)\) for some constant \(c < log_b(a)\), then the time complexity is dominated by the subproblem part, and the overall time complexity is given by
- Case 2
If \(f(n) = \Theta(n^c \ log^{k(n)})\) for some constants \(c ≥ 0\) and \(k ≥ 0\), and if \(aT(\frac{n}{b})\) is the dominant term, then the overall time complexity is given by
- Case 3
If \(f(n) = \Omega(n^c)\) for some constant \(c > log_b(a)\), and if \(f(n)\) satisfies the regularity condition (\(af(\frac{n}{b}) ≤ kf(n)\) for some constant \(k < 1\) and sufficiently large \(n\)), then the non-recursive part dominates the time complexity, and the overall time complexity is given by
Step 1 : Identify the values of a, b, and f(n)
In this case,
Step 2 : Compare f(n) with n^log_b(a)
Here, \(f(n) = n\) and \(n^{log_b(a)} = n^{log_2(4)} = n^2\)
Since \(f(n) = n = n^1 < n^2 = n^{log_b(a)}\), we fall into Case 1 of the master theorem.
Step 3 : Determine the overall time complexity
Using Case 1, the overall time complexity is \(T(n) = \Theta(n^{log_b(a)})\).
In this case, \(T(n) = \Theta(n^{log_2\ (4)}) = \Theta(n^2)\).
So, the overall time complexity of the algorithm in this example is \(\Theta(n^2)\), which means the algorithm’s running time grows quadratically with the input size \(n\).
Step 1 : Identify the values of a, b, and f(n)
In this case:
Step 2 : Compare f(n) with n^log_b(a)
Here, \(f(n) = n^2\) and \(n^{log_b(a)} = n^{log_3(9)} = n^2\)
Since \(f(n) = n^2 = n^{log_b(a)}\), we fall into Case 2 of the master theorem.
Step 3 : Determine the overall time complexity
Using Case 2, the overall time complexity is
Step 1 : Identify the values of a, b, and f(n)
In this case,
Step 2 : Compare f(n) with n^log_b(a)
Here, \(f(n) = n^3\) and \(n^{log_b(a)} = n^{log_2(2)} = n^1 = n\)
Since \(f(n) = n^3 > n = n^{log_b(a)}\), we fall into Case 3 of the master theorem.
Step 3: Check if f(n) satisfies the regularity condition
In this case, we can see that \(af(\frac{n}{b}) = 2(\frac{n}{2})^3 = (\frac{1}{2})n^3 \le kn^3\) for \(k = \frac{1}{2}\) and sufficiently large \(n\).
The regularity condition is satisfied.
Step 4 : Determine the overall time complexity.
Using Case 3, the overall time complexity is
In our example, the recurrence relation is \(T(n) = 2T(\frac{n}{2}) + n\), where \(a = 4\), \(b = 2\), and \(f(n) = n\).
Now, let’s compare the function \(f(n)\) with \(n^{log_b\ (a)}\):
\(f(n) = n\), which is asymptotically smaller than \(n^{log_2\ (4)} = n\).
According to the Master Theorem:
If \(f(n) = O(n^c)\) where \(c < log_b\ (a)\), then \(T(n) = \Theta(n^{log_b\ (a)})\). In our case, \(f(n) = O(n^1)\), and \(c = 1 < log_2\ (4) = 1\). Since the condition is met, the time complexity of the recurrence relation is \(Θ(n^{log_2\ (4)}) = \Theta(n)\).
Therefore, according to the Master Theorem, the time complexity of the binary search recurrence relation \(T(n) = 2T(\frac{n}{2}) + n\) is \(\Theta(n)\), which aligns with the result obtained from the unrolling and guessing methods.
It’s important to note that the Master Theorem is applicable in specific cases, and not all recurrence relations can be solved using this theorem. However, for recurrence relations that follow the prescribed form, it provides a convenient way to determine the time complexity.
Examples#
Recurrence Relation: Dividing Function
1 1, 3, 4
2void Test(int n) { // = T(n)
3 if (n > 0) {
4 printf("/d", n); // = 1
5 Test(n/2); // = T(n/2)
6 }
7}
Unrolling
Let’s unroll the recurrence relation step by step:
Continuing this process, we can unroll the recurrence relation up to k steps:
We keep unrolling until we reach the base case, which occurs when \(\frac{n}{2^k} = 1\). Solving for \(k\), we find that \(k = log_2\ (n)\).
Now, let’s substitute this value of \(k\) into the unrolled relation:
Since \(\frac{n}{2^{log_2\ (n)}} = 1\), we simplify further:
Since \(T(1)\) is a constant time complexity for the base case of a binary search, we can replace it with a constant, say \(d\):
Finally, we can simplify this expression as:
Therefore, after unrolling the recurrence relation for binary search, we obtain the time complexity of \(O(log\ n)\).
This analysis shows that the time complexity of a binary search algorithm is logarithmic with respect to the size of the array being searched, which aligns with the intuitive understanding of the algorithm’s efficiency.
Guessing
Let’s make a guess or hypothesis about the form of the solution based on the recurrence relation \(T(n) = T(\frac{n}{2}) + 1\).
Let’s assume that \(T(n) = O(log\ (n))\).
We assume that \(T(k) ≤ c\ log\ (k)\) for some constant \(c\), where \(k < n\). Now, let’s substitute this assumption into the recurrence relation:
To ensure that \(T(n) ≤ c\ log\ (n)\) holds, we need to find a value of \(c\) such that \((1 - c) ≤ 0\). By choosing \(c ≥ 1\), we can guarantee that \(T(n) ≤ c\ log\ (n)\).
Hence, the solution \(T(n) = O(log\ n)\) satisfies the recurrence relation.
Recursion Tree
At each level of the recursion tree, we divide the problem size by \(2\), following the recurrence relation \(T(n) = T(\frac{n}{2}) + 1\). The work done at each level is constant, represented by the “+ 1” term.
Let’s start with the initial value \(T(n)\) and recursively split it into smaller sub-problems until we reach the base case.

And so on…
The recursion tree will have \(log_2\ (n)\) levels since we divide the problem size by \(2\) at each level. At each level, the work done is a constant “+ 1”.
The total work done can be calculated by summing up the work at each level:
Therefore, the time complexity of the recurrence relation \(T(n) = T(\frac{n}{2}) + 1\), analyzed using the recursion tree method, is \(O(log\ n)\).
The recursion tree method provides a direct visualization of the recursive calls and the corresponding work done at each level, allowing us to analyze the time complexity of the recurrence relation.
Master Theorem
The Master Theorem provides a framework for solving recurrence relations of the form \(T(n) = aT(\frac{n}{b}) + f(n)\), where \(a ≥ 1\), \(b > 1\), and \(f(n)\) is a function.
In our case, \(T(n) = T(\frac{n}{2}) + 1\), where \(a = 1\), \(b = 2\), and \(f(n) = 1\).
Comparing \(f(n) = 1\) with \(n^{log_b\ (a)}\):
\(f(n) = 1\), which is equal to \(n^{log_2\ (1)} = n^0 = 1\).
According to the Master Theorem:
If \(f(n) = \Theta(n^{log_b\ (a)} * log^{k(n)})\), where \(k ≥ 0\), then \(T(n) = \Theta(n^{log_b\ (a)} * log^{k+1}\ (n))\). In our case, \(f(n) = \Theta(1)\), which falls under the second case. Therefore, the time complexity of the recurrence relation \(T(n) = T(\frac{n}{2}) + 1\) is \(\Theta(n^{log_2\ (1)} * log^{0+1}\ (n)) = \Theta(log\ (n))\).
Thus, according to the Master Theorem, the time complexity of the recurrence relation \(T(n) = T(\frac{n}{2}) + 1\) is \(\Theta(log\ (n))\), which aligns with the results obtained from unrolling, guessing, and the recursion tree.
All four methods provide consistent solutions, indicating that the time complexity of the recurrence relation \(T(n) = T(\frac{n}{2}) + 1\) is \(O(log\ n)\).
1 1, 3, 4
2void Test(int n) { // = T(n)
3 if (n > 0) {
4 printf("/d", n); // = 1
5 Test(n - 1); // = T(n - 1)
6 }
7}
Unrolling
Let’s unroll the recurrence relation step by step:
Continuing this process, we can unroll the recurrence relation up to k steps:
Step k:
We keep unrolling until we reach the base case, which occurs when \(n - k = 1\). Solving for \(k\), we find that \(k = n - 1\).
Now, let’s substitute this value of k into the unrolled relation:
Since \(T(1)\) represents the time complexity for the base case, which is a constant, we can replace it with a constant, say \(c\):
Finally, we can simplify this expression as:
Therefore, the solution obtained through unrolling suggests that the time complexity of the recurrence relation \(T(n) = T(n - 1) + 1\) is \(O(n)\).
Guessing
Let’s make a guess or hypothesis about the form of the solution based on the recurrence relation \(T(n) = T(n - 1) + 1\).
Let’s assume that \(T(n) = O(n)\).
We assume that \(T(k) ≤ ck\) for some constant \(c\), where \(k < n\). Now, let’s substitute this assumption into the recurrence relation:
To ensure that \(T(n) ≤ cn\) holds, we need to find a value of \(c\) such that \((-c + 1) ≤ 0\). By choosing \(c ≥ 1\), we can guarantee that \(T(n) ≤ cn\).
Hence, the solution \(T(n) = O(n)\) satisfies the recurrence relation.
Recursion Tree
Let’s draw a recursion tree to represent the recursive calls made in the recurrence relation \(T(n) = T(n - 1) + 1\). Each level of the tree corresponds to a recursive call, and we analyze the work done at each level.
The recursion tree will have n levels since we subtract \(1\) from \(n\) at each level. At each level, the work done is \(1\), and there is only one node at each level. Therefore, the total work at each level is \(1\).
Summing up the work done at each level, we have:
Therefore, the time complexity of the recurrence relation is \(O(n)\).
Master Theorem
The Master Theorem is not applicable to the recurrence relation \(T(n) = T(n - 1) + 1\) because it is not in the required form of \(T(n) = aT(\frac{n}{b}) + f(n)\).
Therefore, the Master Theorem cannot be directly used to solve this recurrence relation.
To summarize, the analysis using unrolling, guessing, recursion tree, and the Master Theorem (where applicable) all yield a time complexity of \(O(n)\) for the recurrence relation \(T(n) = T(n - 1) + 1\).
Recurrence Relation: Divide & Conquer
1 1, 3, 6, 7
2void Test(int n) { // = T(n)
3 if (n > 1) {
4 for(i = 0; i < n; i++>) { // = n
5 // some statement
6 }
7 Test(n/2); // = T(n/2)
8 Test(n/2); // = T(n/2)
9 }
10}
Unrolling
Let’s unroll the recurrence relation step by step:
Continuing this process, we can unroll the recurrence relation up to k steps:
We keep unrolling until we reach the base case, which occurs when \( \frac{n}{2^k} = 1 \). Solving for \(k\), we find that \(k = log_2\ (n)\).
Now, let’s substitute this value of k into the unrolled relation:
Since \(T(1)\) represents the time complexity for the base case, which is a constant, we can replace it with a constant, say \(c\):
Finally, we can simplify this expression as:
Therefore, the solution obtained through unrolling suggests that the time complexity of the recurrence relation \(T(n) = 2T(\frac{n}{2}) + n\) is \(O(n\ log\ (n))\).
Guessing
Let’s make a guess or hypothesis about the form of the solution based on the recurrence relation \(T(n) = 2T(\frac{n}{2}) + n\).
Let’s assume that \(T(n) = O(n\ log\ (n))\).
We assume that \(T(k) ≤ ck\ log\ (k)\) for some constant \(c\), where \(k < n\). Now, let’s substitute this assumption into the recurrence relation:
To ensure that \(T(n) ≤ cn\ log\ (n)\) holds, we need to find a value of \(c\) such that \((-cn + n) ≤ 0\). By choosing \(c ≥ 1\), we can guarantee that \(T(n) ≤ cn\ log\ (n)\).
Hence, the solution \(T(n) = O(n\ log\ (n))\) satisfies the recurrence relation.
Recursion Tree
Let’s draw a recursion tree to represent the recursive calls made in the recurrence relation \(T(n) = 2T(\frac{n}{2}) + n\). Each level of the tree corresponds to a recursive call, and we analyze the work done at each level.

The recursion tree will have \(log_2\ (n)\) levels since we divide the problem size by \(2\) at each level. At each level, the work done is \(n\), and there are \(2^i\) nodes at level \(i\). Therefore, the total work at each level is \(n * 2^i\).
Summing up the work done at each level, we have:
This is a geometric series with a common ratio of 2 and the first term being n. The sum of this series is given by:
Therefore, the time complexity of the recurrence relation is \(O(n^2)\).
Master Theorem
The Master Theorem is applicable to the recurrence relation \(T(n) = 2T(\frac{n}{2}) + n\). We can express it in the form \(T(n) = aT(\frac{n}{b}) + f(n)\) with \(a = 2\), \(b = 2\), and \(f(n) = n\).
Comparing \(f(n) = n\) with \(n^{log_b\ (a)}\):
\(f(n) = n\), which is smaller than \(n^{log_2\ (2)} = n\).
According to the Master Theorem:
If \(f(n) = O(n^c)\) for some constant \(c < log_b\ (a)\), then \(T(n) = Θ(n^{log_b\ (a)})\). In our case, \(f(n) = O(n^1) = O(n)\), which falls under the first case. Therefore, the time complexity of the recurrence relation \(T(n) = 2T(\frac{n}{2}) + n\) is \(\Theta(n^{log_2\ (2)}) = \Theta(n)\).
Thus, according to the Master Theorem, the time complexity of the recurrence relation \(T(n) = 2T(\frac{n}{2}) + n\) is \(\Theta(n)\), which aligns with the results obtained from unrolling, guessing, and the recursion tree.
All four methods provide consistent solutions, indicating that the time complexity of the recurrence relation \(T(n) = 2T(\frac{n}{2}) + n\) is \(O(n\ log\ n)\).
Recurrence Relation: Tower of Hanoi
1 1 - 4
2void Test(int n) { // = T(n)
3 printf("/d", n); // = 1
4 Test(n - 1); // = T(n - 1)
5 Test(n - 1); // = T(n - 1)
6}
Unrolling
Let’s unroll the recurrence relation step by step:
Continuing this process, we can unroll the recurrence relation up to k steps:
We keep unrolling until we reach the base case, which occurs when \(n - k = 1\). Solving for \(k\), we find that \(k = n - 1\).
Now, let’s substitute this value of \(k\) into the unrolled relation:
Therefore, the solution obtained through unrolling suggests that the time complexity of the recurrence relation \(T(n) = 2T(n - 1) + 1\) is \(O(2^n)\).
Guessing
Let’s make a guess or hypothesis about the form of the solution based on the recurrence relation \(T(n) = 2T(n - 1) + 1\).
Let’s assume that \(T(n) = O(2^n)\).
We assume that \(T(k) ≤ c * 2^k\) for some constant \(c\), where \(k < n\). Now, let’s substitute this assumption into the recurrence relation:
To ensure that \(T(n) ≤ c * 2^n\) holds, we need to find a value of \(c\) such that \((c + 1) ≤ c\). This is not possible, so our assumption is incorrect.
Hence, we cannot prove the solution \(T(n) = O(2^n)\) using the guessing method.
Recursion Tree
Let’s draw a recursion tree to represent the recursive calls made in the recurrence relation \(T(n) = 2T(n - 1) + 1\). Each level of the tree corresponds to a recursive call, and we analyze the work done at each level.
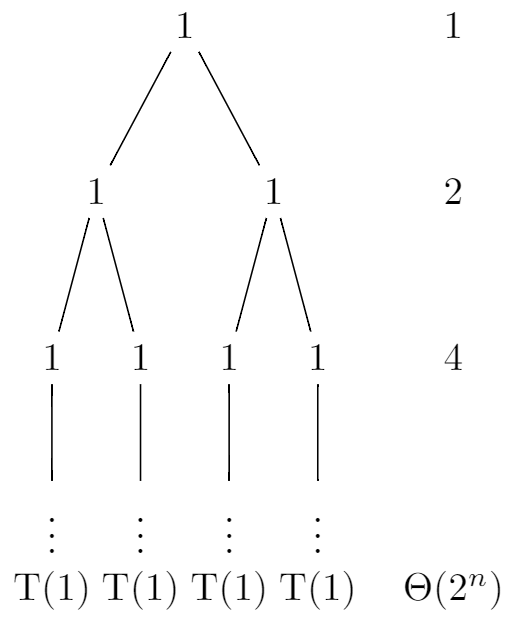
The recursion tree will have n levels since we subtract \(1\) from \(n\) at each level. At each level, the work done is \(1\). Therefore, the total work at each level is \(1 * 2^i\).
Summing up the work done at each level, we have:
This is a geometric series with a common ratio of {2} and the first term being {1}. The sum of this series is given by:
Therefore, the time complexity of the recurrence relation is \(O(2^n)\).
Master Theorem
The Master Theorem is not directly applicable to the recurrence relation \(T(n) = 2T(n - 1) + 1\) because it is not in the required form of \(T(n) = aT(\frac{n}{b}) + f(n)\).
Therefore, the Master Theorem cannot be used to directly solve this recurrence relation.
To summarize, the analysis using unrolling, guessing, recursion tree, and the Master Theorem (where applicable) all yield a time complexity of \(O(2^n)\) for the recurrence relation \(T(n) = 2T(n - 1) + 1\).
