MTH 180 Concepts#

Additional Resources

Disclaimer

The following sets of videos have been vetted for the general knowledge of mathematical subject matter applicable to CSC 212 but not directly focused on. This is not an exhaustive list, but a guide to helpful instruction. The variety in selection is merely to help fit the multitude of learning curves for students within the course.

Pre-calculas w/ Professor Leonard
The Organic Chemistry Tutor
Prof D
TrevTutor & Kimberly Brehm

Sequences#

Sequence#

a function whose domain is the set of positive integers
ex: \(\{ 1, 2, 3, 4, \dots \}\)

The general, or \(n^{th}\) term, is denoted as \(a_n\)

\(odd\ integers\)

\(1\)

\(3\)

\(5\)

\(7\)

\(9\)

\(\dots\)

\(n\)

\(perfect\ squares\)

\(1\)

\(4\)

\(9\)

\(16\)

\(25\)

\(\dots\)

\(n\)

\(a_1\)

\(a_2\)

\(a_3\)

\(a_4\)

\(a_5\)

\(\dots\)

\(a_n\)

Try it

Write out the first five (5) terms of the sequence…

\(a_n = 2n + 3\)
\[\begin{split}\begin{align} a_1 & = 2(1) + 3 & = 5 \\ a_2 & = 2(2) + 3 & = 7 \\ a_3 & = 2(3) + 3 & = 9 \\ a_4 & = 2(4) + 3 & = 11 \\ a_5 & = 2(5) + 3 & = 13 \\ \end{align}\end{split}\]
\[first\ five\ (5)\ terms\ of\ the\ sequence\ \]
\[ \{ 5, 7, 9, 11, 13 \} \]
\(a_n = (-1)^n * \frac{6 - 2n}{ \sqrt{n + 1}} \)
\[\begin{split}\begin{align} a_1 & = (-1)^{1} * \frac{6 - 2(1)}{ \sqrt{(1) + 1}} \\ & = \frac{-4}{\sqrt{-2}} \\ & = \frac{-4 \sqrt{-2}}{2} \\ & = -2 \sqrt{-2} \\ \end{align}\end{split}\]
\[\begin{split}\begin{align} a_2 & = (-1)^{2} * \frac{6 - 2(2)}{ \sqrt{(2) + 1}} \\ & = \frac{2}{\sqrt{3}} \\ & = \frac{2 \sqrt{3}}{3} \\ \end{align}\end{split}\]
\[\begin{split}\begin{align} a_3 & = (-1)^{3} * \frac{6 - 2(3)}{ \sqrt{(3) + 1}} \\ & = \frac{-0}{\sqrt{4}} \\ & = 0 \\ \end{align}\end{split}\]
\[\begin{split}\begin{align} a_4 & = (-1)^{4} * \frac{6 - 2(4)}{ \sqrt{(4) + 1}} \\ & = \frac{-2}{\sqrt{5}} \\ & = \frac{-2 \sqrt{5}}{5} \\ \end{align}\end{split}\]
\[\begin{split}\begin{align} a_5 & = (-1)^{5} * \frac{6 - 2(5)}{ \sqrt{(5) + 1}} \\ & = - \frac{-4}{\sqrt{6}} \\ & = \frac{2 \sqrt{6}}{3} \\ \end{align}\end{split}\]
\[first\ five\ (5)\ terms\ of\ the\ sequence\ \]
\[ \{ -2 \sqrt{-2}, \frac{2 \sqrt{3}}{3}, 0, \frac{-2 \sqrt{5}}{5}, \frac{2 \sqrt{6}}{3} \} \]

Try it

Write the \(n^{th}\) term of the sequence \(\{a_n\}\) suggested by the pattern

\(\frac{2}{3}, \frac{4}{9}, \frac{8}{27}, \frac{16}{81}, \dots \)

Find the pattern…

\(\frac{2^1}{3^1}, \frac{2^2}{3^2}, \frac{2^3}{3^3}, \frac{2^4}{3^4} \)

Therefore,

\[\begin{split}\begin{align} a_n & = \frac{2^n}{3^n} \\ & = \bigg( \frac{2}{3} \bigg) ^n \\ \end{align}\end{split}\]
\( 2, -4, 6, -8, 10, \dots \)

Find the pattern…

\(2\)

\(-4\)

\(6\)

\(-8\)

\(10\)

\(\dots\)

\(n\)

\(a_1\)

\(a_2\)

\(a_3\)

\(a_4\)

\(a_5\)

\(\dots\)

\(a_n\)
Check : \(a_n = (-1)^n * 2n\)
\[\begin{split}\begin{align} a_1 & = (-1)^1 * 2(1) \\ & = \bbox[5px,border:2px solid red]{ \cancel{-2} } \end{align}\end{split}\]
Check : \(a_n = (-1)^{n+1} * 2n\)
\[\begin{split}\begin{align} a_1 & = (-1)^{n+1} * 2(1) \\ & = -1^2 * 2 \\ & = \bbox[5px,border:2px solid green]{ 2 } \end{align}\end{split}\]

Therefore,

\[\begin{split}\begin{align} a_n = (-1)^{n+1} * 2n \\ \end{align}\end{split}\]
Recursive relation#

a sequence for which the given is the first term together with a rule for obtaining any \(a_{n+1}\) from the preceding term \(a_n\) for \(n \ge 1\)

Try it

Find the first five (5) terms of the recursively defined infinite sequence

\(a_1 = 2, \ \ \ \ \ a_{n+1} = - \frac{n}{a_n}\)
\[\begin{split}\begin{align} a_1 & = 2 \\ \end{align}\end{split}\]
\[a_2\]
\[\begin{split}\begin{align} a_{n+1} & = a_2 \\ a_2 & = \frac{-1}{a_1} \\ & = \frac{-1}{2} \\ a_{n+1} & = a_3 \\ \end{align}\end{split}\]
\[a_3\]
\[\begin{split}\begin{align} a_3 & = \frac{-2}{a_2} \\ & = \frac{-2}{\frac{-1}{2}} \\ & = 4 \\ \end{align}\end{split}\]
\[a_4\]
\[\begin{split}\begin{align} a_4 & = \frac{-3}{a_3} \\ & = \frac{-3}{4} \\ \end{align}\end{split}\]
\[a_5\]
\[\begin{split}\begin{align} a_5 & = \frac{-4}{a_4} \\ & = \frac{-4}{(\frac{-3}{4})} \\ & = \frac{16}{3} \\ \end{align}\end{split}\]
\[first\ five\ recursive\ terms\]
\[\begin{split}\begin{align} \frac{-1}{2}, 4, \frac{-3}{4}, \frac{16}{3} \ \ \ \ \ \\ \end{align}\end{split}\]
\(a_1 = -1, \ \ \ \ \ a_2 = 1, \ \ \ \ \ a_n = a_{n+1} + na_{n-1}\)
\[\begin{split}\begin{align} a_1 & = -1 \\ a_2 & = 1 \\ \end{align}\end{split}\]
\[a_3\]
\[\begin{split}\begin{align} a_3 & = a_{3-2} + (3 * a_{3-1}) \\ & = a_1 + (3 * a_2) \\ & = -1 + 3(1) \\ & = 2 \\ \end{align}\end{split}\]
\[a_4\]
\[\begin{split}\begin{align} a_4 & = a_{4-2} + (4 * a_{4-1}) \\ & = a_2 + (4 * a_3) \\ & = 1 + 4(1) \\ & = 9 \\ \end{align}\end{split}\]
\[a_3\]
\[\begin{split}\begin{align} a_5 & = a_{5-2} + (5 * a_{5-1}) \\ & = a_3 + (5 * a_4) \\ & = 2 + 5(9) \\ & = 47 \\ \end{align}\end{split}\]
\[first\ five\ recursive\ terms\]
\[\begin{split}\begin{align} -1, 1, 4, 9, 47 \\ \end{align}\end{split}\]

Series#

Series#

the sum of a number of terms in a sequence

\[ can\ be\ finite \]
\[ 1 + 3 + 5 + 7 \]
\[ can\ be\ infinite \]
\[ 1 + 3 + 5 + 7 + \bbox[5px,border:2px solid green]{ \dots } \]
\[ 1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \bbox[5px,border:2px solid green]{ \dots } \]
Summation / Sigma Notation
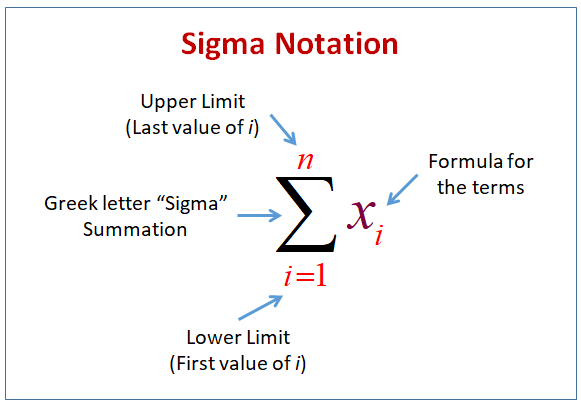
https://knowledgeuniverseonline.com/wp-content/uploads/2022/03/sigma-notation.png
\[\begin{split} k-index\ of \\ summation \end{split}\]

\(n\) = stopping point
\( \sum \) = \(sigma\) or “sum of”
\(k\) = starting point
\(a_k\) = formula for each term

Example

\[ \sum_{k=1}^{n} a_k = a_1 + a_2 + a_3 + a_4 + \dots + a_{n-1} + a_n \]

Try it

Write out each sum (expand and simplify)

\( \sum_{k=1}^{6} \frac{3}{k+1} \)
\[\begin{split}\begin{align} \sum_{k=1}^{6} \frac{3}{k+1} & = \frac{3}{1+1} + \frac{3}{2+1} + \frac{3}{3+1} + \frac{3}{4+1} + \frac{3}{5+1} + \frac{3}{6+1} \\ & = \frac{3}{2} + 1 + \frac{3}{4} + \frac{3}{5} + \frac{1}{2} + \frac{3}{7} \\ & = \frac{669}{140} \\ \end{align}\end{split}\]

Try it

Express each sum using summation notation

\( 1 + 3 + 5 + 7 + \dots + [2(12)-1] \)
\[\begin{split}\begin{align} & 1 & + & 3 & + & 5 & + & 7 & + & \dots & + & [2(12)-1] \\ & \downarrow & & \downarrow & & \downarrow & & \downarrow & & & & \downarrow \\ & a_1 & + & a_2 & + & a_3 & + & a_4 & + & \dots & + & a_{12} \\ \end{align}\end{split}\]
Check : \(a_k = 2k-1\)
\[\begin{split}\begin{align} a_1 & = 2 * 1 - 1 \\ & = \bbox[5px,border:2px solid green]{ 1 } \\ a_2 & = 2 * 2 - 1 \\ & = \bbox[5px,border:2px solid green]{ 3 } \\ a_3 & = 2 * 3 - 1 \\ & = \bbox[5px,border:2px solid green]{ 5 } \\ a_4 & = 2 * 4 - 1 \\ & = \bbox[5px,border:2px solid green]{ 7 } \\ \end{align}\end{split}\]
Therefore
\[ \bbox[5px,border:2px solid green]{ \sum_{k=1}^{12} 2k-1 } \]

Try it

Find the sum for each sequence

\( \sum_{k=1}^{24} -k \)
\[\begin{split}\begin{align} & = (-1) & + & (-2) & + & (-3) & + & (-4) & + & \dots & + & (-24) \\ & = -(1 & + & 2 & + & 3 & + & 4 & + & \dots & + & 24) \\ & = \frac{-24(24+1)}{2} \\ & = -12(25) \\ & = \bbox[5px,border:2px solid green]{ -300 } \\ \end{align}\end{split}\]

Formula

\[ \sum_{k=1}^{n} k = 1 + 2 + 3 + \dots + n = \frac{n(n+1)}{2} \]
\( \sum_{k=137}^{428} 2.1 \)
\[\begin{split}\begin{align} & ( 2.1 + 2.1 + \dots + & 2.1 & ) = (2.1)(292) = \bbox[5px,border:2px solid green]{ 613.2 } \\ & \downarrow & \downarrow \\ & a_{137} & a_{428} & \\ \\ & \ \ \ 428 \\ & \underline{- 137} \\ & \ \ \ 291 \ iterations \end{align}\end{split}\]

Formula

\[\begin{split}\begin{align} \sum_{k=m}^{n} c & = (n - m + 1) c & \\ \sum_{k=137}^{428} 2.1 & = (428 - 137 + 1) 2.1 & \\ \end{align}\end{split}\]

\(c\) = constant

\( \sum_{k=0}^{14} k^2-4 \)
\[\begin{split}\begin{align} & ( 0^2 - 4 ) + ( 1^2 - 4 ) + ( 2^2 - 4 ) + \dots + ( 14^2 - 4 ) = \bbox[5px,border:2px solid green]{ 955 } \\ \end{align}\end{split}\]

Formula

\[\begin{split}\begin{align} \sum_{k=1}^{n} (a_k - b_k) & = \sum_{k=1}^{n} a_k - \sum_{k=1}^{n} b_k\\ \\ \\ \sum_{k=0}^{14} (k^2 - 4) & = \sum_{k=0}^{14} k^2 - \sum_{k=0}^{14} 4 \\ \end{align}\end{split}\]

Breakout 1

\[\begin{split}\begin{align} \sum_{k=1}^{n} k^2 & = 1^2 + 2^2 + 3^2 + \dots + n^2 & = \frac{n(n+1)(2n+1)}{6} & \\ & & = \frac{14 \bigg(14+1 \bigg) \bigg(2(14)+1 \bigg)}{6} & \\ & & = \bbox[5px,border:2px solid green]{ 1015 } & \\ \end{align}\end{split}\]

Breakout 2

\[\begin{split}\begin{align} \sum_{k=1}^{n} 4 & = 4(15) = \bbox[5px,border:2px solid green]{ 60 } \\ \end{align}\end{split}\]

Outcome

\[\begin{split}\begin{align} \sum_{k=0}^{14} (k^2 - 4) & = \sum_{k=0}^{14} k^2 - \sum_{k=0}^{14} 4 \\ & = 1015 - 60 \\ & = \bbox[5px,border:2px solid green]{ 955 } \end{align}\end{split}\]