Left-Leaning Red-Black Trees

Intro

Rotations

Insertions {Strategy}

Insertion {Examples}

Deletions

Delete Fixes

Left-leaning red-black BSTs

Structure

A left-leaning red-black tree is a type of self-balancing binary search tree that maintains the following properties:

• Every node is colored either red or black.

• The root node is always black.

• Every leaf (null node) is considered black.

• If a node is red, both its children are black.

• Every path from a node to its descendant leaves contains the same number of black nodes.

Why Red-Black Trees?

Applications

• Most of the self-balancing BST library functions like map, multiset, and multimap in C++ use Red-Black Trees.

• Implementing CPU Scheduling Linux.

• K-mean clustering algorithm in machine learning for reducing time complexity.

• MySQL also uses the Red-Black tree for indexes on tables in order to reduce the searching and insertion time.

• Implementation of the virtual memory manager in some operating systems, to keep track of memory pages and their usage.

• Many programming languages (such as Java, C++, and Python) have implemented Red Black Trees as a built-in data structure for efficient searching and sorting of data.

• Implementation of graph algorithms such as Dijkstra’s shortest path algorithm and Prim’s minimum spanning tree algorithm.

• Implementation of game engines.

– Geeks For Geeks

Advantages

• Guaranteed time complexity of O(log n) for basic operations like insertion, deletion, and searching.

• Self-balancing.

• Used in a wide range of applications due to their efficient performance and versatility.

• The mechanism used to maintain balance in Red Black Trees is relatively simple and easy to understand.

– Geeks For Geeks

Disadvantages

• Red Black Trees require one extra bit of storage for each node to store the color of the node (red or black).

• Complexity of Implementation.

• Although Red Black Trees provide efficient performance for basic operations, they may not be the best choice for certain types of data or specific use cases.

– Geeks For Geeks

Implementing 2-3 trees with binary trees

Challenge

How to represent a 3-node?

Approach 1

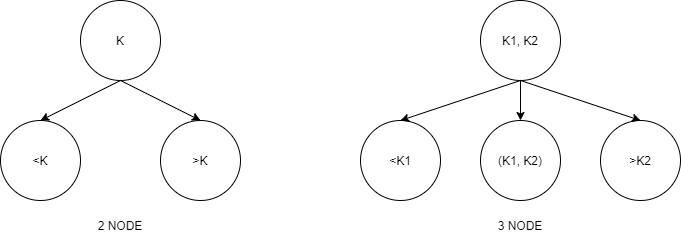
Regular BST

• No way to tell a 3-node from a 2-node

• Can’t (uniquely) map from BST back to 2-3 tree

Approach 2

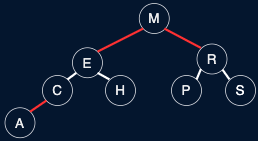
Regular BST with red “glue” nodes

• Wastes space for extra node

• Messy code

Approach 3

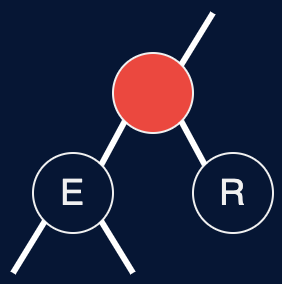
Regular BST with red “glue” links

• Widely used in practice

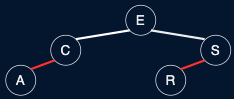
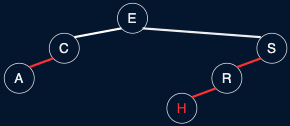
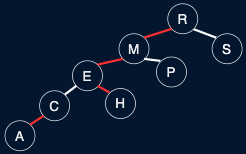
• Arbitrary restriction: red links lean left

1-1 Correspondence

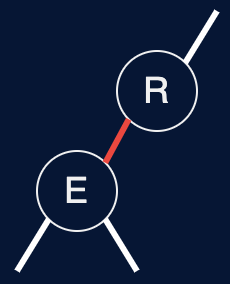
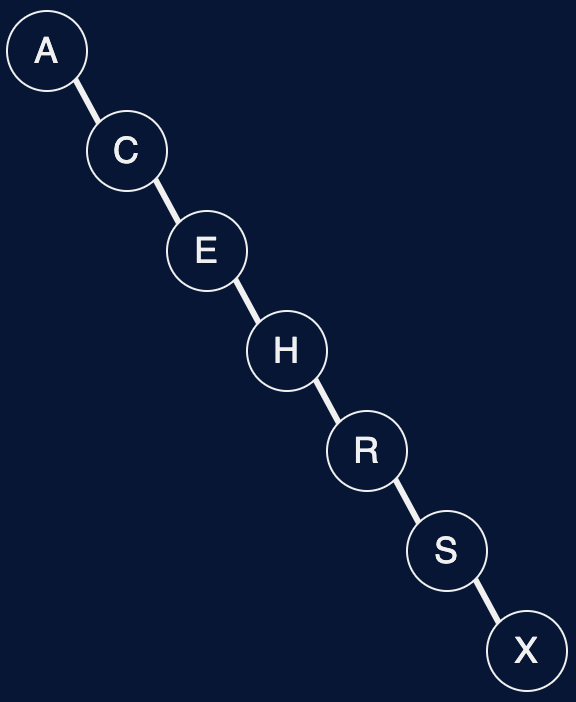
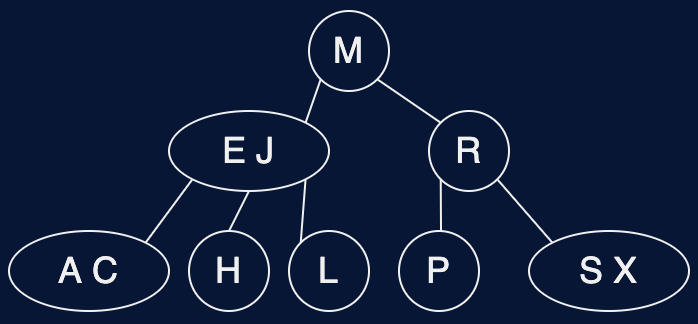
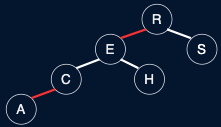
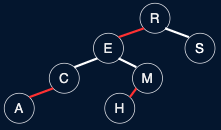
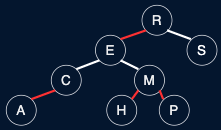
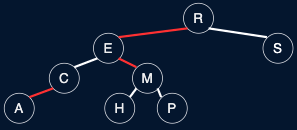
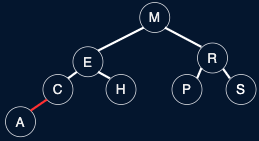
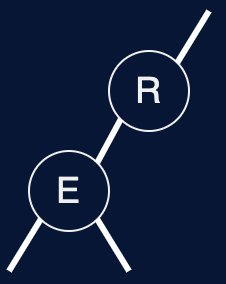
Fig. 39 LLRB Tree v. 2-3 Tree

Definition of LLRB trees (without reference to 2-3)

A BST such that

• No node has two red links connected to it

• Red links lean left

• Every path from root to null has the same number of black links

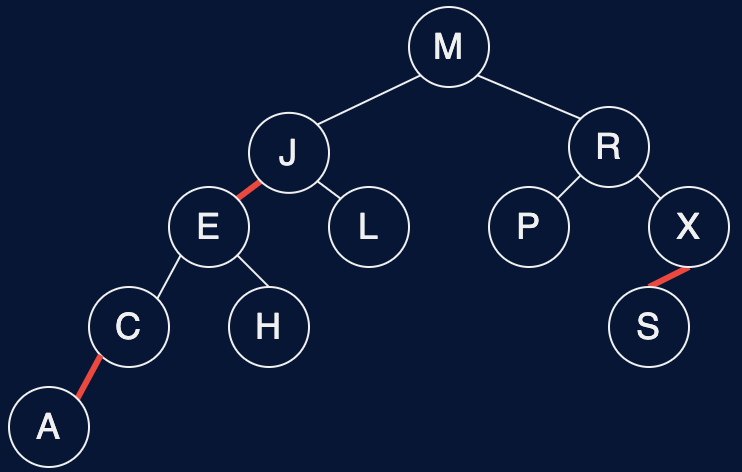
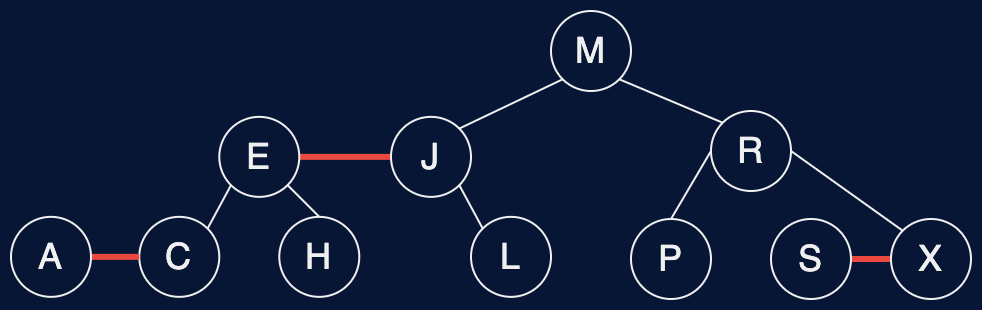
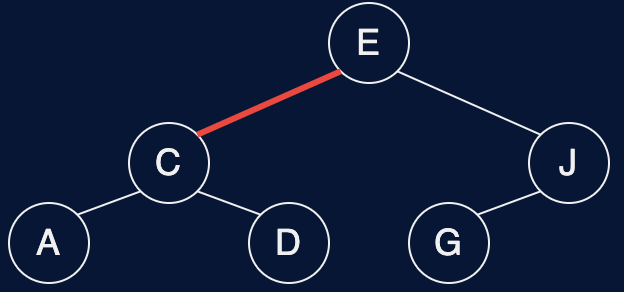
Fig. 40 \(red-black\ tree\)

Search

Observation

Search is the same as for BST (ignore color)

public Value get(Key key) {
  Node x = root;  
  while (x != null) {
    int cmp = key.compareTo(x.key);
    if      (cmp <  0)  x = x.left;
    else if (cmp >  0)  x = x.right;
    else if (cmp == 0)  return x.val;
  }
  return null;
}

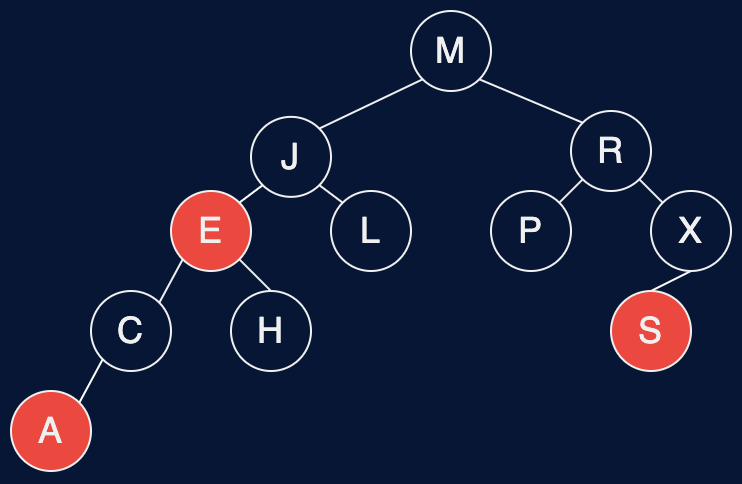
Fig. 41 \(red-black\ tree\)

Remark: Many other ops (floor, iteration, rank, selection) are also identical

Representation

Each node is pointed to by precisely one link (from its parent) \(\Rightarrow\) can encode color of links in nodes

private static final boolean RED   = true;
private static final boolean BLACK = false;

private class Node {
  Key     key;  
  Value   val;
  Node    left;
  Node    right;
  // color of parent link
  Boolean color;
}

private boolean isRed(Node x) {
  // null links are black
  if (x == null) return false;    
  return x.color == red;
}

\[\begin{split}h = root\\\end{split}\]

\[\begin{split}h.left.color\ is\ RED\\\end{split}\]

\[h.right.color\ is\ BLACK\]

The road to LLRB trees

1

Fig. 42 BSTs can get imbalanced

2

Fig. 43 2-3 trees (balanced but awkward to implement)

3

Fig. 44 3-nodes “glued” together with red links

4

Fig. 45 LLRB trees (color in links)

5

Fig. 46 implementing LLRB trees (color in nodes)

Red-Black Tree Operations

Overview

Basic strategy

Maintain 1-1 correspondence with 2-3 trees

During internal operations, maintain

• Symmetric order.

• Perfect black balance.

• [ but not necessarily color invariants ]

To restore color invariants: perform rotations and color flips

Left rotation

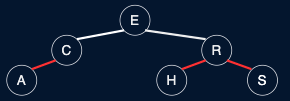
Orient a (temporarily) right-leaning red link to lean left

Pseudocode

private Node rotateLeft(Node h) {
  assert isRed(h.right);
  Node x  = h.right;
  h.right = x.left;
  x.left  = h
  x.color = h.color;
  h.color = RED;
  return x;
}

Rotate E left

Fig. 47 before & after…

Invariants: Maintains symmetric order and perfect balance

Right rotation

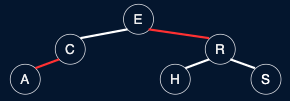
Orient a left-leaning red link to (temporarily) lean right

Pseudocode

private Node rotateRight(Node h) {
  assert isRed(h.right);
  Node x  = h.left;
  h.left  = x.right;
  x.right = h
  x.color = h.color;
  h.color = RED;
  return x;
}

Rotate E right

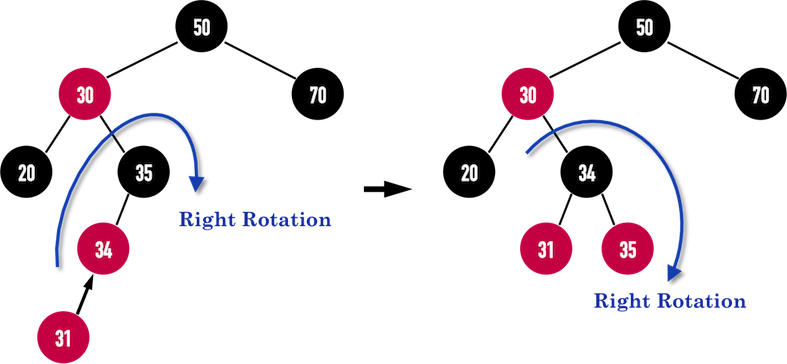
Fig. 48 before & after…

Invariants: Maintains symmetric order and perfect balance

Color flip

Recolor to split a (temporary) 4-node

Pseudocode

private Node colorFlip(Node h) {
  assert isRed(h);
  assert isRed(h.left);
  assert isRed(h.right);
  h.color        = RED;
  h.left.color   = BLACK;
  h.right.color  = BLACK;
}

Color flip

Fig. 49 before & after…

Invariants: Maintains symmetric order and perfect balance

Insertions

Do standard BST insert \(\ \ \ \ \ \ \ \ \ \ \ \ \leftarrow\) preserves symmetric order

Color new link red \(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \leftarrow\) preserve perfect black balance

Repeat up the tree until color invariants restored

• two left red links in a row? \(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \Rightarrow\) rotate right

• left and right links both red? \(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \Rightarrow\) color flip

• right link only red? \(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \Rightarrow\) rotate left

Inserting H

1

Fig. 50 [R]: add new node here

2

Fig. 51 [S]: two lefts in a row, rotate right

3

Fig. 52 [R]: both children red, flip colors

4

Fig. 53 [E]: right link, so rotate left

5

Fig. 54 complete

Inserting P

1

Fig. 55 [M]: add new node here

2

Fig. 56 [M]: both children red, flip colors

3

Fig. 57 right link red, rotate left

4

Fig. 58 two lefts in a row, rotate right

5

Fig. 59 both children red, flip colors

6

Fig. 60 complete

Visualize

Click the image to hyperlink and interact

Implementation

Do standard BST insert and color new link red

Repeat up the tree until color invariants restored

• two left red links in a row? \(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \Rightarrow\) rotate right

• left and right links both red? \(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \Rightarrow\) color flip

• right link only red? \(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \Rightarrow\) rotate left

private Node put(Node h, Key, k, Value v) {
  if (h == null) return new Node(key, val, RED;         // insert at bottom and color red
  
  int cmp = key.compareTo(h.key)
  if      (cmp <  0) h.left = put(h.left, key, val);
  else if (cmp >  0) h.left = put(h.right, key, val);
  else if (cmp == 0) h.val  = val);
  
  // following lines restore color invariants
  if (isRed(h.right) && !isRed(h.left))        h = rotateLeft(h);
  if (isRed(h.left ) && !isRed(h.left.left))   h = rotateRight(h);
  // only a few extra lines of code provides near-perfect balance
  if (isRed(h.left ) && isRed(h.right))        h = flipColors(h);           
  
  return h;
}

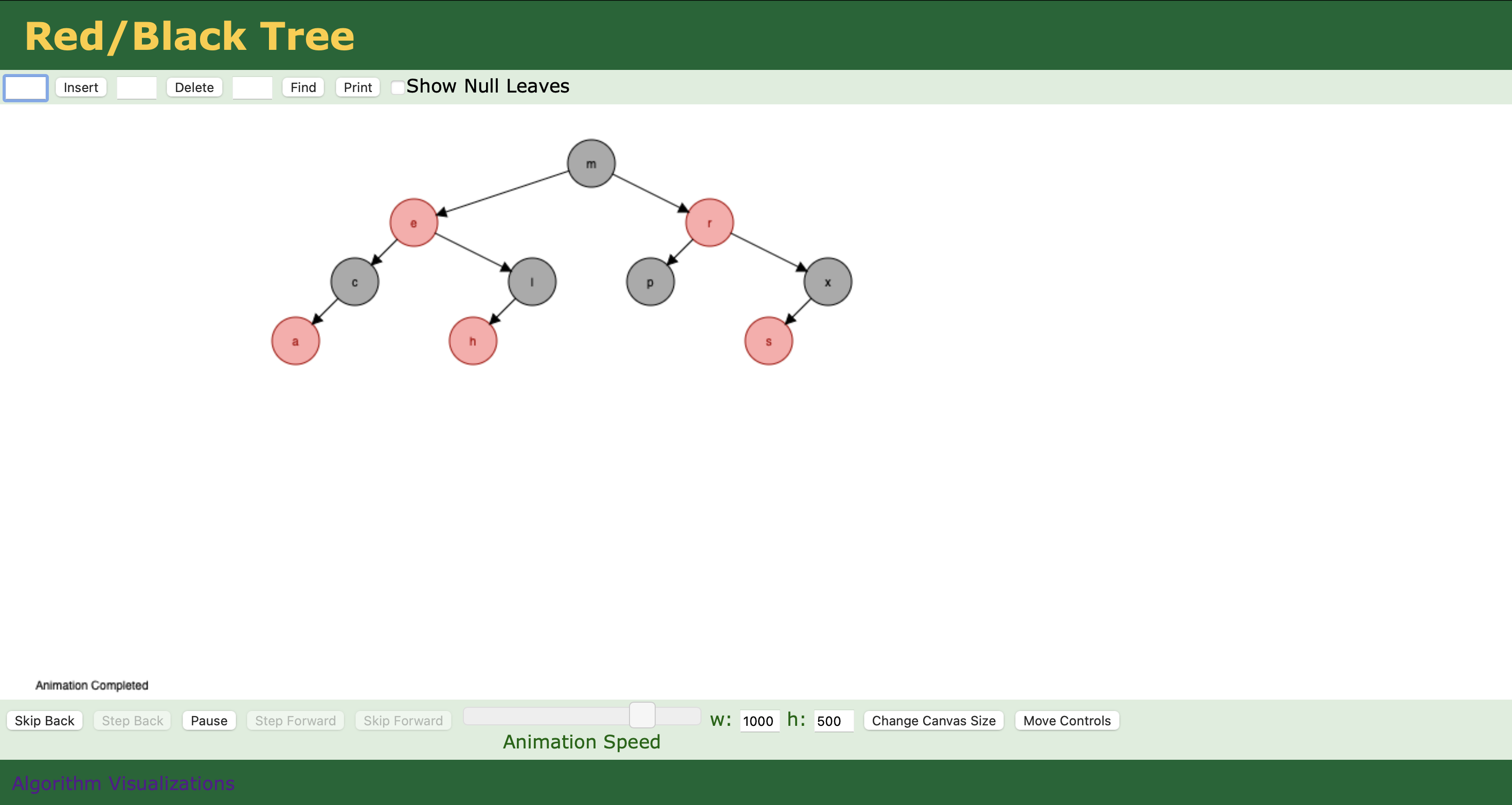
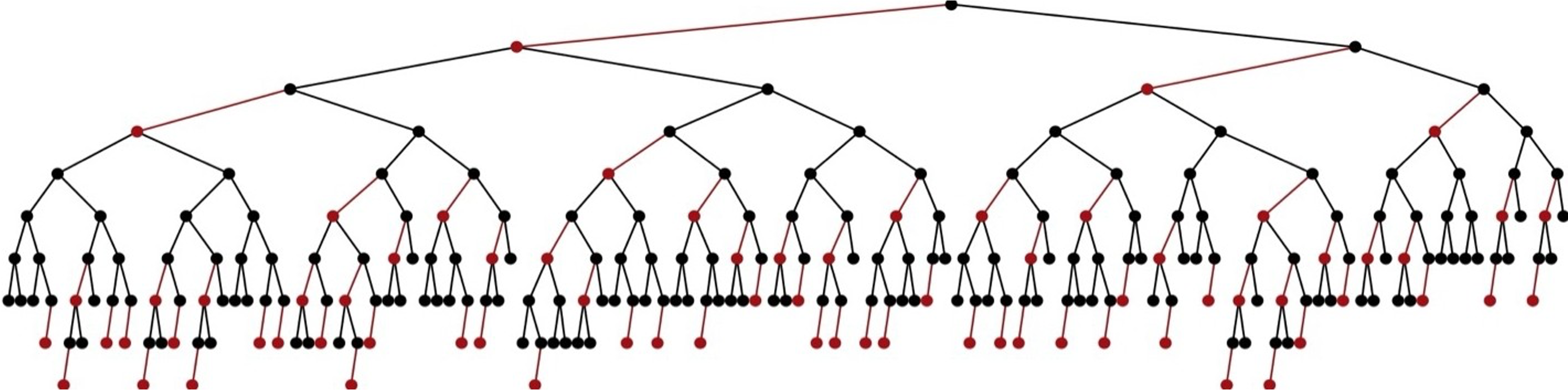
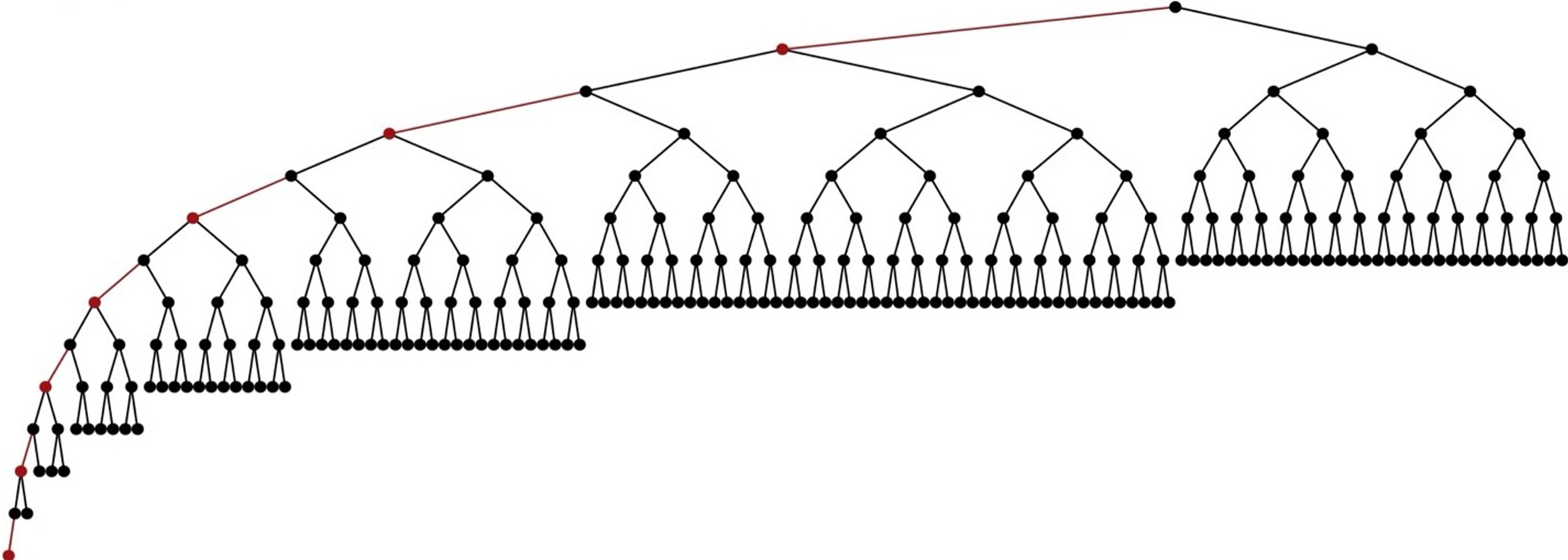
Visualizations | \(n=255\)

Random order

\(height = 9\)
\(average\ depth = 6.3\)

Fig. 61 random

Ascending order

\(height = 7\)
\(average\ depth = 6.0\)

Fig. 62 ascending

Descending order

\(height = 13\)
\(average\ depth = 6.5\)

Fig. 63 descending

Balance

Proposition

Height of corresponding 2-3 tree is \(\le log_2\ n\)

Proof

• Black height = height of corresponding 2-3 tree \(\le log_2\ n\)

• Never two red links in a row
  \(\ \ \ \ \ \Rightarrow\) height of LLRB tree \(\le (2 \times black\ height) + 1 \le 2\ log_2\ n\)

• [A slightly more refined argument show \(height\ \le 2\ log_\ n\)]

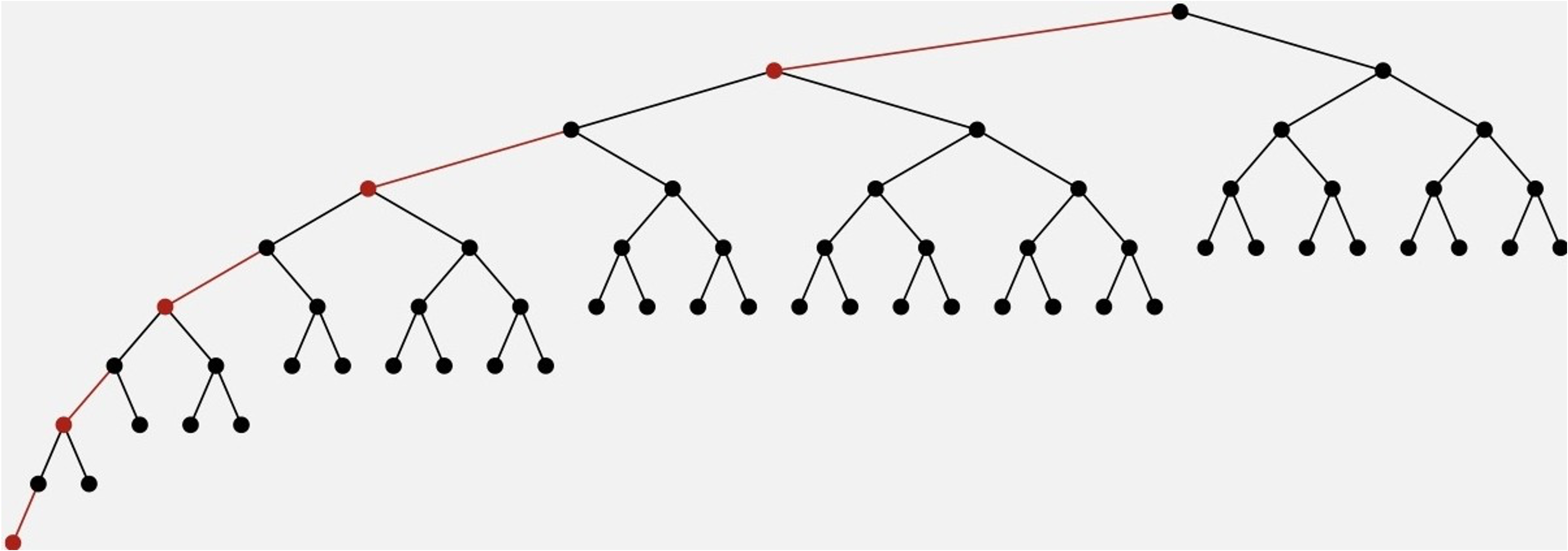
Fig. 64 \(height\ \le 2\ log_2\ n\)

Summary

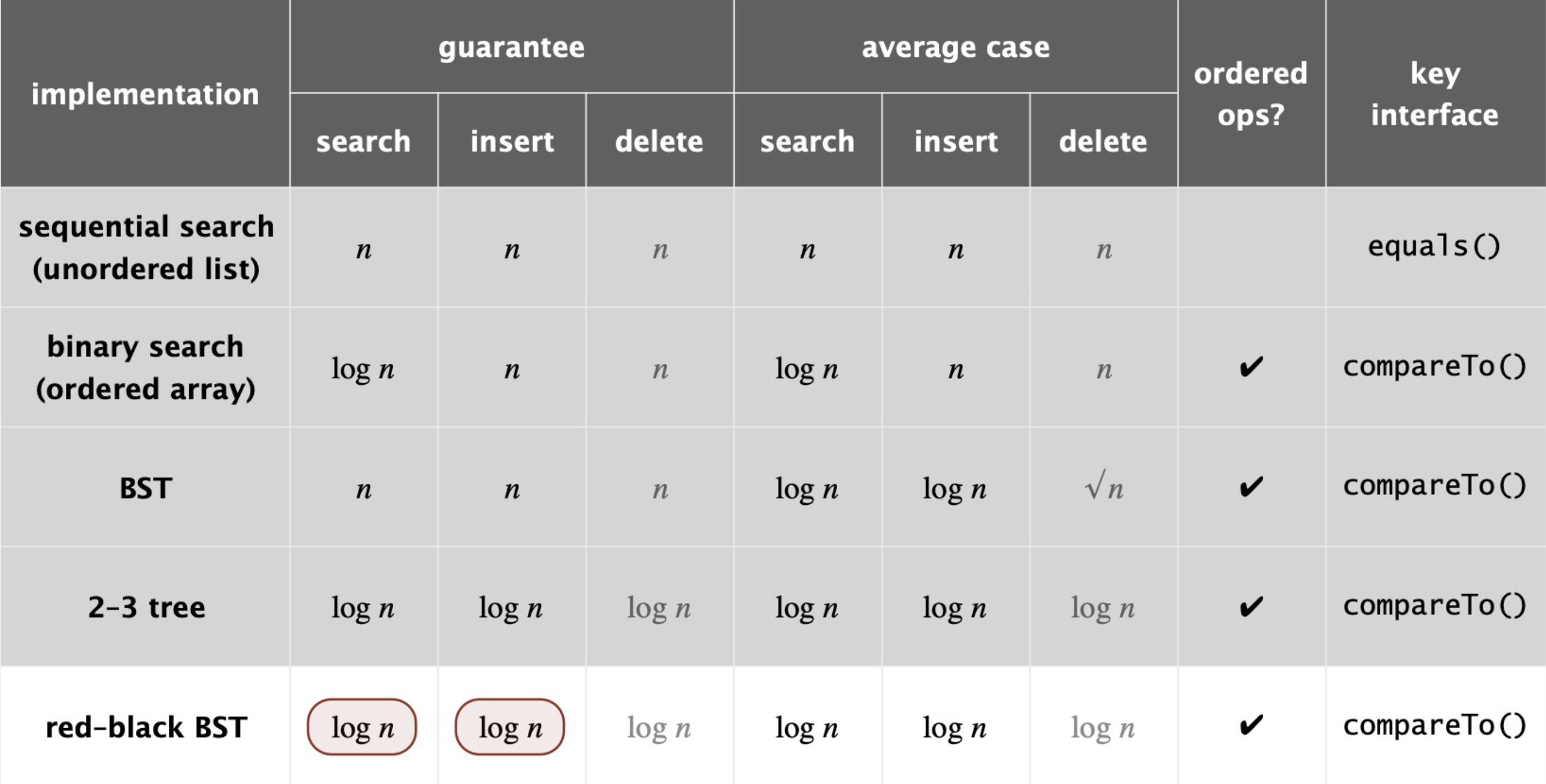
Fig. 65 hidden constant \(c\) is small for r-b BST
(at most \(2\ log_2\ n\) compares)