Quicksort

Quick Sort

Divide the array into two partitions (subarrays)

• need to pick a pivot and rearrange the elements into two partitions

Conquer Recursively each half

• call Quick Sort on each partition (i.e. solve 2 smaller problems)

Combine Solutions

• there is no need to combine the solutions

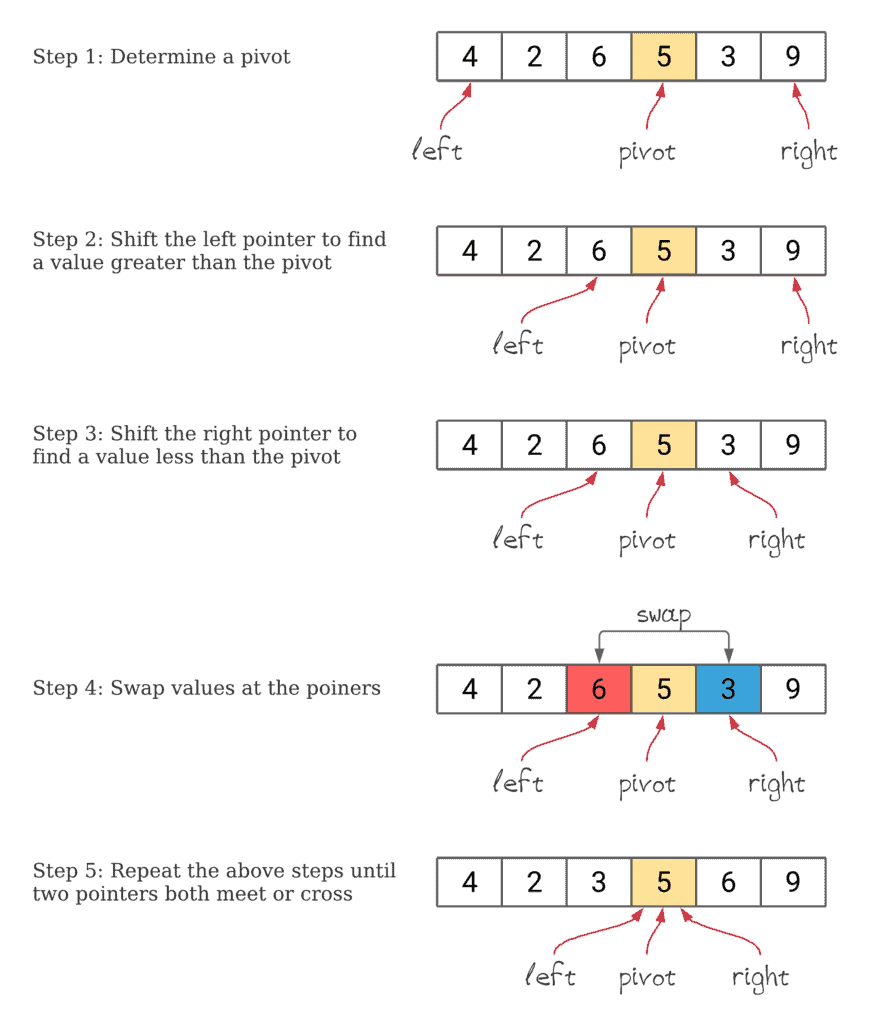
Partition

Partition: algorithm

Implementation

quicksort

void quicksort(int *A, int n, int m)              
{
    // shuffle the array  
    std::random_shuffle(A, A + n);
    
    // call recursive quicksort  
    r_quicksort(A, 0, n - 1);
}

r_quicksort

void r_quicksort(int *A,int lo, int  hi)                                           
{
    if (hi <= lo) return;
    
    int p = partition(A, lo, hi);  
    
    r_quicksort(A, lo, p - 1);  
    
    r_quicksort(A, p + 1, hi);
}

partition

int partition (int *A, int lo, int hi)                      
{
    int i = lo;
    int j = hi + 1;  
    while (1) {
      
        // while A[i] < pivot, increase i 
        while (A[++i] < A[lo])
            if (i == hi) break;

        // while A[i] > pivot, decrease j 
        while (A[lo] < A[--j])
            
            if (j == lo) break;
          
            // if i and j cross exit theloop
            if(i >= j) break;
            
            // swap A[i] and A[j]
            std::swap(A[i], A[j]);
    }
    // swap the pivot with A[j]  
    std::swap(A[lo], A[j]);

    //return pivot's position
    return j;
}

Visualize

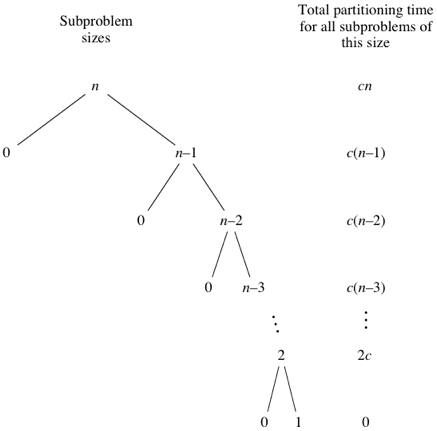
Analysis of Quick Sort

Worst-Case

\[\begin{split} c \{ n + (n-1) + (n-2) + (n-3) + ... 1 \} \\ c * \frac{n(n+1)}{2} \\ = \Theta(n^2) \end{split}\]

input sorted, reverse order, equal elements

\[\begin{split}\begin {align} T(n) &= T(n - 1) + T(0) + \Theta(n) \\ &= T(n - 1) + \Theta(1) + \Theta(n) \\ &= T(n - 1) + \Theta(n) \\ &= \dots \\ &= \Theta(n^2) \\ \end {align}\end{split}\]

can shuffle or randomize the array (to avoid the worst-case)

Best-Case

• pivot partitions array evenly (almost never happens)

\[\begin{split} \begin {align} T(n) &= 2T(\frac{n}{2}) + \Theta(n) \\ &= \dots \\ &=\ \Theta(n\ log\ n) \end {align}\end{split}\]

Average-Case

• analysis is more complex

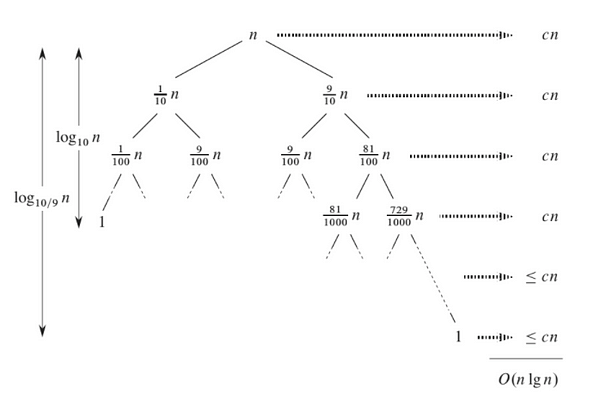
• Consider a 9-to-1 proportional split

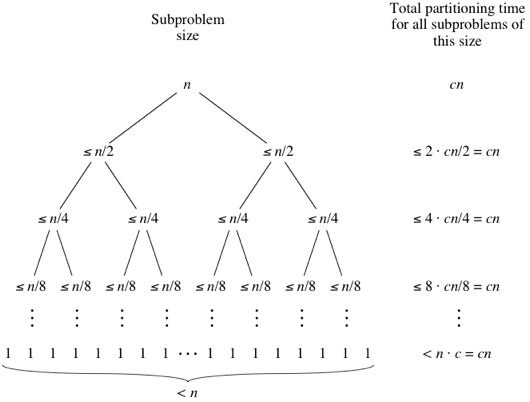
• Even a 99-to-1 split yields same running time

• Faster than merge sort in practice (less data movement)

\[\begin{split}\begin {align} T(n) &= T(\frac{n}{10}) + T(\frac{9n}{10}) + \Theta(n) \\ &= \dots \\ &= \Theta(n\ log\ n) \\ \end {align}\end{split}\]

Add all \(cn\) from side of tree with greatest depth (right subtree):

\[\begin{split} = cn * log_{\frac{10}{9}}\ n \\ = \Theta(n\ log\ n) \\ \end{split}\]

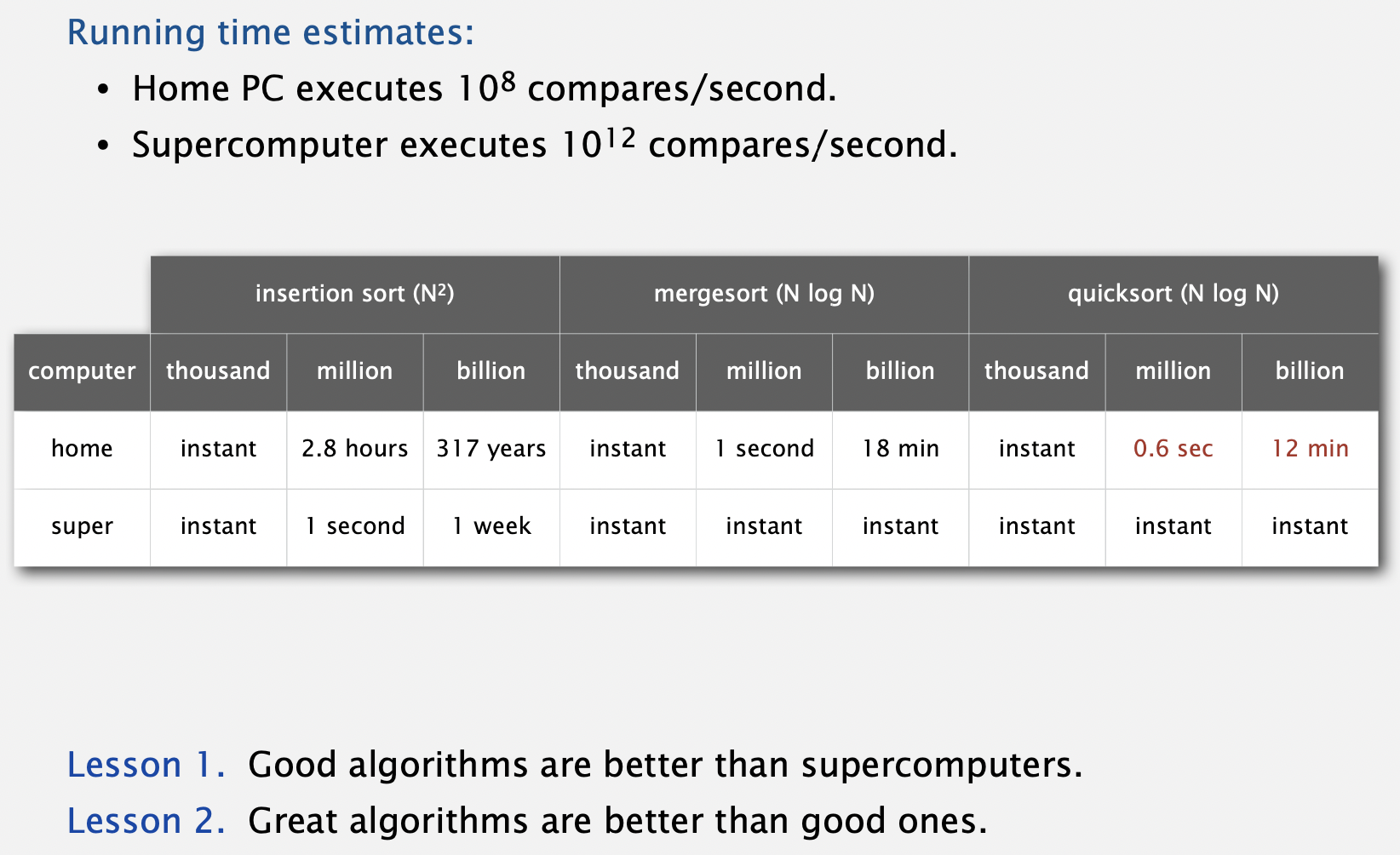
Comments on Quick Sort

Properties

• it is in-place but not stable

• benefits substantially from code tuning

Improvements

use insertion sort for small arrays

• avoid overhead on small instances (~10 elements) median of 3 elements

• estimate true median by inspecting 3 random elements three-way partitioning

• create three partitions \( \le pivot\), \(== pivot\), \( \ge pivot\)

Sorting Algorithms

incomplete

	Best-Case	Average-Case	Worst-Case	Stable	In-place
Selection Sort
Insertion Sort
Merge Sort
Quick Sort

complete

	Best-Case	Average-Case	Worst-Case	Stable	In-place
Selection Sort	\(n^2\)	\(n^2\)	\(n^2\)	No	Yes
Insertion Sort	\(n\)	\(n^2\)	\(n^2\)	Yes	Yes
Merge Sort	\(n\ log\ n\)	\(n\ log\ n\)	\(n\ log\ n\)	Yes	No
Quick Sort	\(n\ log\ n\)	\(n\ log\ n\)	\(n^2\)	No	Yes

Empirical Analysis

https://www.cs.princeton.edu/courses/archive/spring18/cos226/lectures/23Quicksort.pdf