Maps

Define

A map is a data structure that associates unique keys with values. It enables efficient storage and retrieval of data, where each key is mapped to a corresponding value.

An unordered_map is a data structure in C++ that is part of the Standard Template Library (STL). It is an associative container that provides an unordered collection of key-value pairs. The keys in an unordered_map are unique, and it allows for efficient storage and retrieval of data, similar to a dictionary. Unlike a map, it does not store elements in a specific order, making it more efficient for some operations.

Use Cases

map

Databases

Maps are used in database indexing to swiftly retrieve records based on unique keys, such as primary keys.

Symbol Tables

Compilers and interpreters employ maps to store identifiers (e.g., variable names) and associated attributes (e.g., data types).

Caches

Maps are used in caching mechanisms to quickly access cached data. Keys typically represent URLs, file paths, or query results.

Network Routing

In networking, maps are utilized to map destination addresses to routes for efficient packet forwarding.

unordered_map

Caching

unordered_map can be used in caching mechanisms where keys represent queries or frequently accessed data, and values are the cached results.

Frequency Counting

It is helpful in counting the frequency of elements in a dataset, for example, counting word occurrences in a text corpus.

Configuration Settings

Storing configuration parameters in an unordered_map is common, where keys represent setting names and values store corresponding values.

Graph Algorithms

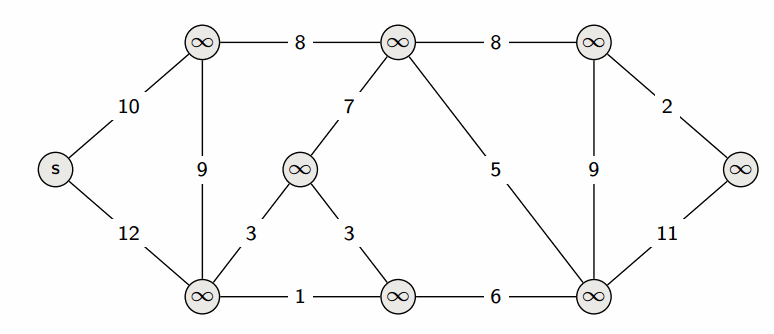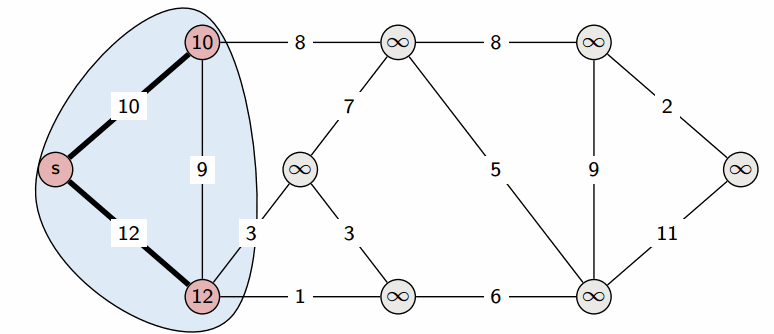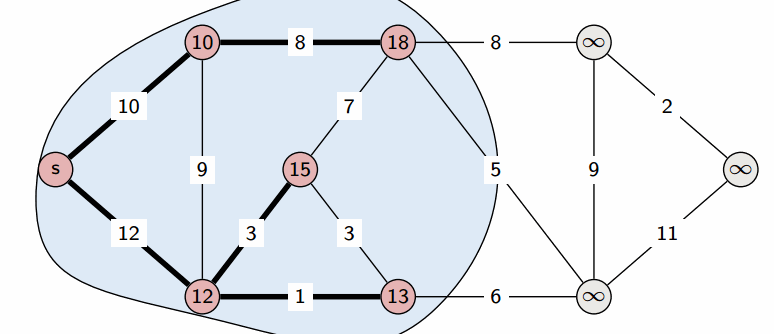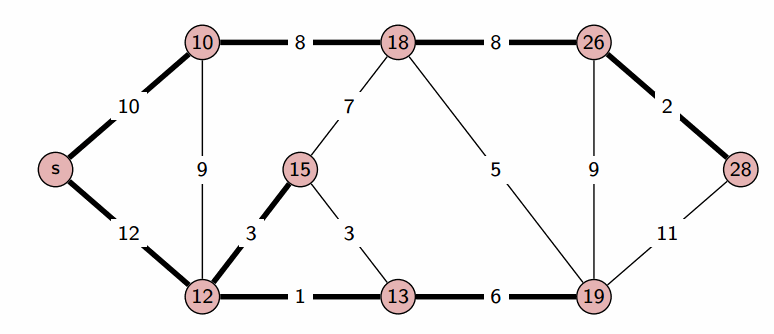
In graph algorithms like Dijkstra’s algorithm, an unordered_map can be used to track the shortest distance to each vertex.

Advantages & Disadvantages

Advantages

Efficient Retrieval {both}

Maps provide fast access to values based on their keys.

Customization {both}

You have control over the data structure, allowing for customization.

Versatility {map}

They can store various data types as values.

Enforces Uniqueness {map}

Maps ensure that keys are unique.

Hash-based {unordered_map}

It is implemented as a hash table, making it highly efficient for most operations.

Dynamic Sizing {unordered_map}

It automatically resizes when needed, which can be more memory-efficient.

Disadvantages

Memory Overhead {both}

Hash tables used to implement maps may consume more memory due to internal data structures.

Hash Collisions {map}

Handling multiple keys mapping to the same index can lead to performance issues.

Not Ideal for Range Queries {map}

Maps are not designed for range-based searches, which could be inefficient.

Complexity for Custom Objects {unordered_map}

Defining a hash function for custom objects can be complex.

Unordered {unordered_map}

As the name implies, it does not maintain any specific order of elements.

Programming

CppRef: map

Pseudo- map

1. Create a Map class.
2. Initialize an array for storing key-value pairs.
3. Define a hash function to map keys to array indices.
4. Implement functions for key-value operations:
   - Insert(key, value): Calculate the hash, store the (key, value) pair.
   - Get(key): Calculate the hash, return the corresponding value.
   - Remove(key): Calculate the hash, remove the (key, value) pair.

Code- map

Define a Map class with an array to store key-value pairs.
The Hash function calculates the index in the array for a given key using a simple hashing algorithm.
Insert adds a key-value pair to the map, Get retrieves a value by key, and Remove deletes a key-value pair.
The main function demonstrates usage.

#include <iostream>
#include <vector>

const int arraySize = 100; // Choose an appropriate size

class Map {
public:
    Map() {
        mapArray.resize(arraySize);
    }

    void Insert(std::string key, int value) {
        int index = Hash(key);
        mapArray[index] = std::make_pair(key, value);
    }

    int Get(std::string key) {
        int index = Hash(key);
        return mapArray[index].second;
    }

    void Remove(std::string key) {
        int index = Hash(key);
        mapArray[index] = std::make_pair("", 0);
    }

private:
    std::vector<std::pair<std::string, int>> mapArray;

    int Hash(std::string key) {
        int hash = 0;
        for (char c : key) {
            hash = (hash * 31 + c) % arraySize;
        }
        return hash;
    }
};

int main() {
    Map map;
    map.Insert("apple", 5);
    map.Insert("banana", 3);

    std::cout << "Value of 'apple': " << map.Get("apple") << std::endl;
    map.Remove("banana");

    return 0;
}

Value of `apple`: 5 

CppRef: unordered_map

Pseudo- unordered_map

Note: Creating a pseudocode for unordered_map can be challenging due to the internal complexity of a hash table. However, here’s a simplified version

1. Create an UnorderedMap class.
2. Initialize a hash table with empty buckets.
3. Implement a hash function to map keys to buckets.
4. Implement functions for key-value operations:
   - Insert(key, value): Calculate the hash, store the (key, value) pair in the corresponding bucket.
   - Get(key): Calculate the hash, retrieve the value from the corresponding bucket.
   - Remove(key): Calculate the hash, remove the (key, value) pair from the corresponding bucket.

Code- unordered_map

Include the unordered_map header to use the unordered_map data structure.
Create an unordered_map called frequency_map with keys as strings and values as integers. Insert key-value pairs, access values by keys, and remove a key-value pair.

#include <iostream>
#include <unordered_map>
#include <string>

int main() {
    std::unordered_map<std::string, int> frequency_map;

    // Insert key-value pairs
    frequency_map["apple"] = 3;
    frequency_map["banana"] = 2;

    // Access values by key
    std::cout << "Frequency of 'apple': " << frequency_map["apple"] << std::endl;

    // Remove a key-value pair
    frequency_map.erase("banana");

    return 0;
}

Compare

	std::map	std::unordered_map
Data Structure	Red-Black Tree	Hash Table
Order of Elements	Sorted (based on keys)	Unordered (no specific order)
get	\(O(log\ n)\)	\(O(1)\) average, \(O(n)\) worst-case
insert	\(O(log\ n)\)	\(O(1)\) average, \(O(n)\) worst-case
remove	\(O(log\ n)\)	\(O(1)\) average, \(O(n)\) worst-case
Memory Usage	Higher memory consumption	Lower memory consumption
Custom Key Types	Requires operator< for keys	Requires a hash function
Range Iteration	Efficient	Less efficient
Use Cases	When elements need to be sorted or ordered	When fast access times are critical, order doesn’t matter

Note: assume a well-designed/distributed hash function and minimal collisions. In practice, worst-case scenarios should also be considered, leading to amortized \(O(1)\) performance for many operations