Queues

TL;DR

A queue is another linear data structure in computer science that follows the First-In-First-Out (FIFO) principle. This means that the element that is added first to the queue is the first element to be removed from it.

A queue is similar to a queue of people waiting in line, where the person who enters the queue first is the first person to leave. The queue data structure has two primary operations: enqueue and dequeue. The enqueue operation adds an element to the end of the queue, while the dequeue operation removes the front-most element from the queue.

Queues are commonly used in programming for various purposes, such as job scheduling, breadth-first search, and buffer management. In job scheduling, a queue is used to schedule tasks or processes for execution based on their priority or arrival time. In breadth-first search, a queue is used to traverse a graph or tree in a level-by-level manner. In buffer management, a queue is used to manage the flow of data between two processes or devices.

Additional Resources

• Data Structures: Stacks and Queues | HackerRank

Basic Operations

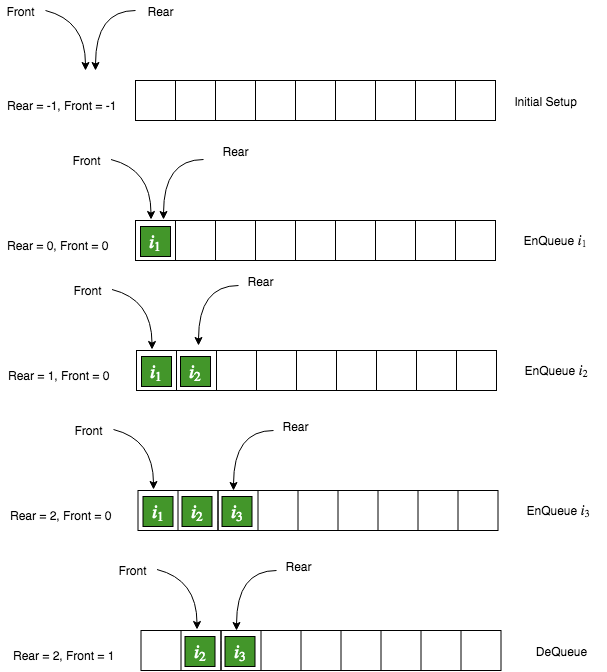
enqueue

• inserts one element onto the queue

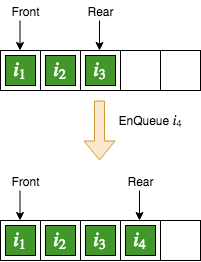
The enqueue operation inserts a new item at the rear end of the queue. After the enqueue operation, the value of rear is increased by 1.

– https://algorithmtutor.com/Data-Structures/Basic/Queues/

dequeue

• returns the element at the top of the queue (and removes it)

The dequeue operation removes the item at the front of the queue. When we remove the item at the front, we increase the value of front.

– https://algorithmtutor.com/Data-Structures/Basic/Queues/

isEmpty

not necessary, but sometimes useful

Documentation

CPPRef

Sample

#include <stack>
#include <iostream>

int main() {
    std::queue<int> q1;
    q1.push(5);
    std::cout << q1.size() << "\n";
    
    std::queue<int> q2(q1);
    std::cout << s.size() << "\n";
    
    std::deque<int> deq { 3, 1, 4, 1, 5 };
    std::queue<int> q3(deq);
    std::cout << q3.size() << "\n";
    return 0;
}

1
1
5

Implementation : Array

Array

• enqueue and dequeue at different ends of the array (easier and efficient)

• can be fixed-length

• can also use a dynamic array (grows over time)

  • additional cost for dynamic arrays

Sample

void enqueue(Queue* queue, int item)
{
  if (isFull(queue))
    return;
  queue->rear = (queue->rear + 1)
                % queue->capacity;
  queue->array[queue->rear] = item;
  queue->size = queue->size + 1;
  cout << item << " enqueued to queue\n"; 
}

int dequeue(Queue* queue)
{
  if (isEmpty(queue))
    return INT_MIN;
  int item = queue->array[queue->front];  
  queue->front = (queue->front + 1)
                  % queue->capacity;
  queue->size = queue->size - 1;
  return item;
}

https://www.geeksforgeeks.org/queue-set-1introduction-and-array-implementation/

Visualize

https://www.cs.usfca.edu/~galles/visualization/QueueArray.html

May take a moment to load…

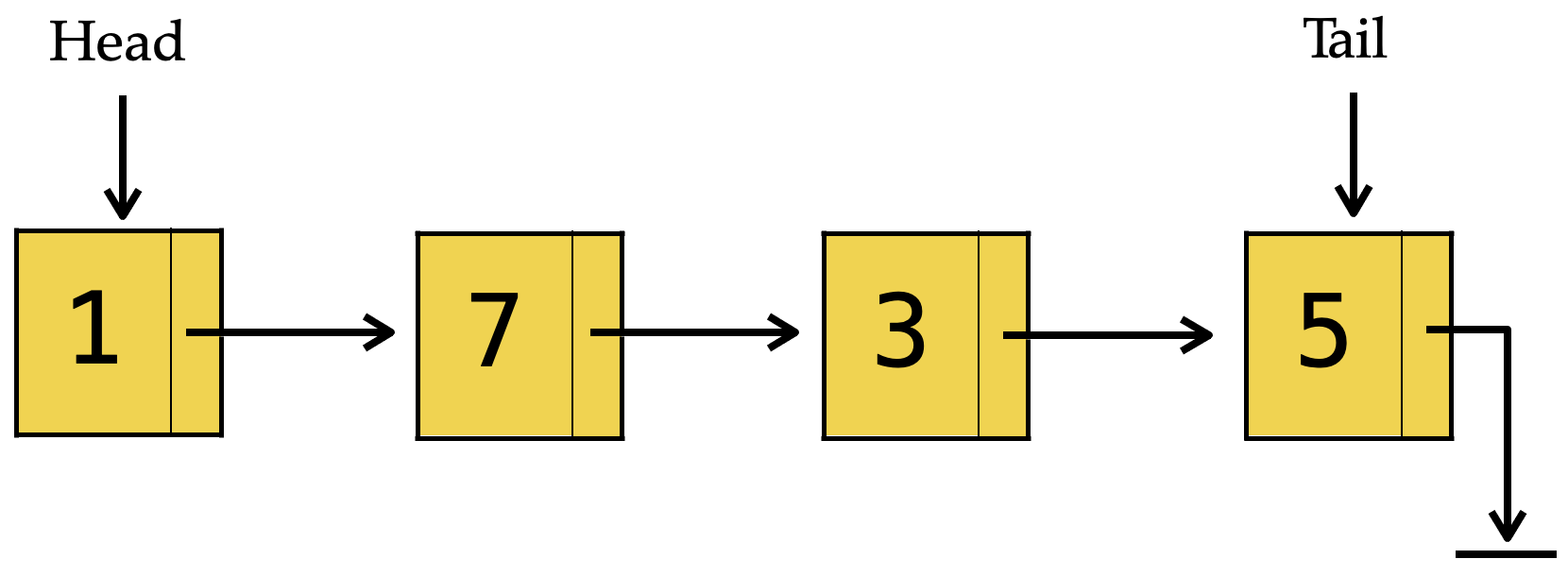
Implementation : Linked List

LL

• enqueue and dequeue at different ends

https://www.cs.usfca.edu/~galles/visualization/QueueArray.html

Sample

void enQueue(int x)
{
  QNode* temp = new QNode(x);     

  if (rear == NULL) {
    front = rear = temp;
    return;
  }

  rear->next = temp;
  rear = temp;
}

void deQueue()
{
  if (front == NULL)
    return;

  QNode* temp = front;  
  front = front->next;

  if (front == NULL)
    rear = NULL;

  delete (temp);
}

https://www.geeksforgeeks.org/queue-linked-list-implementation/

Visualize

May take a moment to load…

Considerations

Underflow

error can be thrown when calling dequeue on an empty queue

Overflow

error can be thrown when calling enqueue on a full queue (especially in fixed-length implementations)

Applications

Media Playlists (Youtube, Spotify, Music,etc.)

Process management in Operating Systems

Simulations

Used in other algorithms

etc…

Time & Space Complexity

Operation	Best	Average	Worst	Space
\(isEmpty()\)	\(O(1)\)	\(O(1)\)	\(O(1)\)	\(O(1)\)
\(enqueue()\)	\(O(1)\)	\(\color{red}{O(n)}\)	\(\color{red}{O(n)}\)	\(O(1)\)
\(dequeue()\)	\(O(1)\)	\(\color{red}{O(n)}\)	\(\color{red}{O(n)}\)	\(O(1)\)
\(count()\)	\(O(1)\)	\(\color{red}{O(n)}\)	\(\color{red}{O(n)}\)	\(O(1)\)
\(peek()\)	\(O(1)\)	\(O(1)\)	\(O(1)\)	\(O(1)\)
\(show()\)	\(O(1)\)	\(\color{red}{O(n)}\)	\(\color{red}{O(n)}\)	\(O(1)\)

---

Note: there is no advantage in using an array versus a linked list for this structure…