Mergesort#
Merge sort is a popular sorting algorithm that works by recursively dividing an array into two halves until each half contains only one element, and then merging the two halves in a sorted manner. The algorithm divides the array in half, sorts each half recursively, and then merges the two sorted halves.
The key idea behind merge sort is that it’s easier to sort two smaller sorted arrays than to sort one large unsorted array. As a result, merge sort can achieve a better time complexity than some other sorting algorithms, such as bubble sort or insertion sort.
The time complexity of merge sort is \(O(n\ log\ n)\) in the worst case, where n is the number of elements to be sorted. This makes merge sort one of the most efficient comparison-based sorting algorithms, and it’s widely used in practice.
Divide & Conquer#
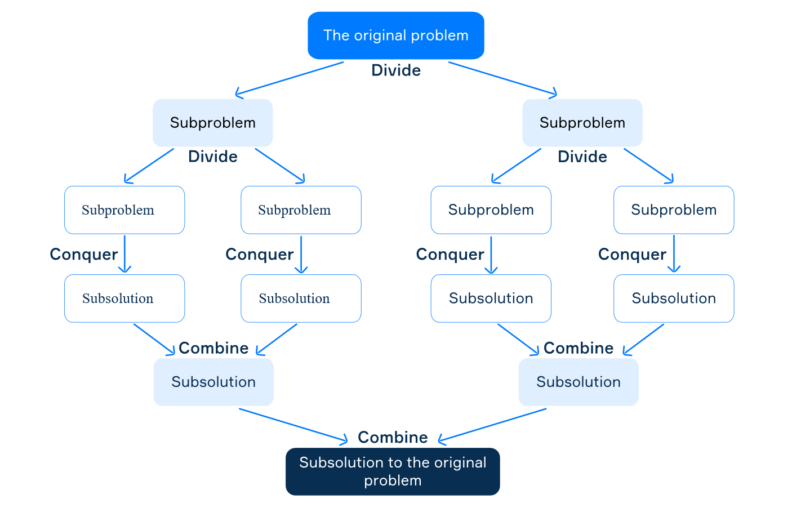
Divide the problem into smaller subproblems
Conquer recursively
… each subproblem
Combine Solutions
sorting with insertion sort is \(n^2\)
we can divide the array into two halves and sort them separately
each subproblem could be sorted in \(≈\frac{n^2}{4}\)
sorting both halves will require \(≈2\frac{n^2}{4}\) 🤔
we need an additional operation to combine both solutions
Time “reduced” from \(≈n^2\) to \(≈\frac{n^2}{2}+n\)
Merge Sort#
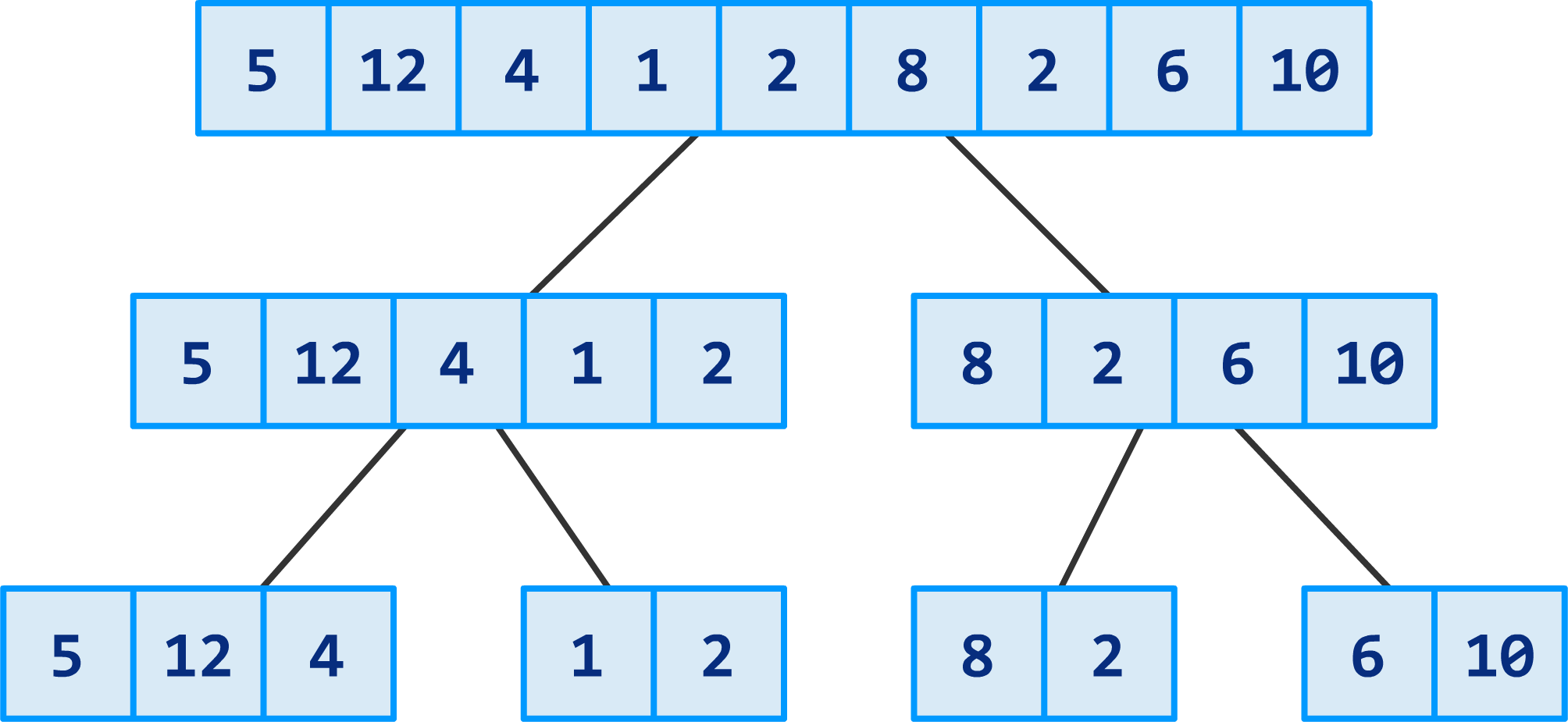
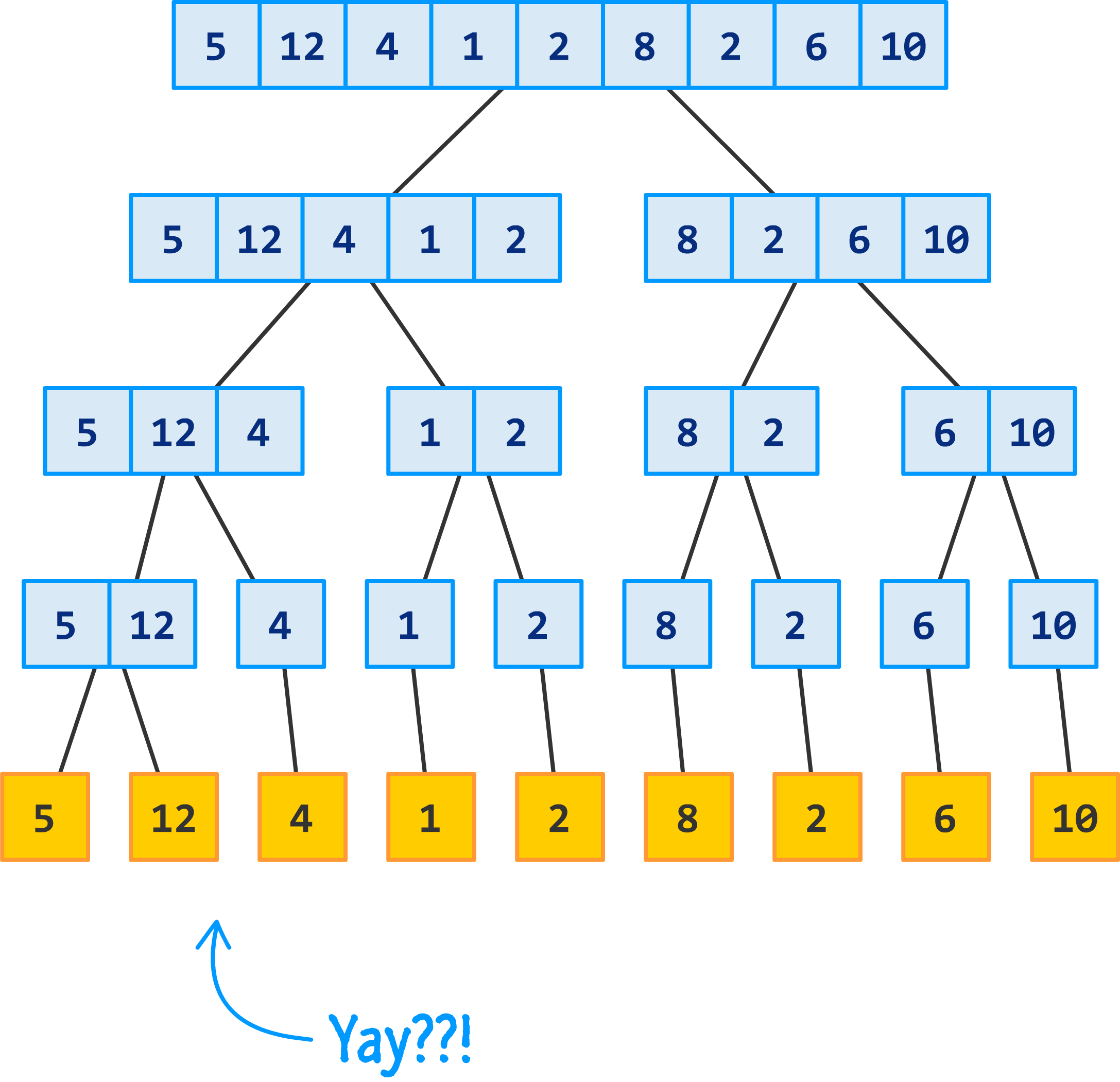
Divide the array into two halves
just need to calculate the midpoint
Conquer Recursively each half
call Merge Sort on each half (i.e. solve 2 smaller problems)
Merge Solutions
after both calls are finished, proceed to merge the solutions
1MergeSort(arr[], lo, hi)
2
3if (hi <= lo) return;
4
5 // Find the middle point to divide the array into two halves:
6 int mid = lo + (hi - lo) / 2;
7
8 // Call mergeSort for first half:
9 mergesort(A, lo, mid);
10
11 // Call mergeSort for second half:
12 mergesort(A, mid + 1, hi);
13
14 // Merge the two halves sorted in steps 2 and 3:
15 merge(A, lo, mid, hi);
1void mergesort(int *A, int n) {
2 int *aux = new int[n];
3 r_mergesort(A, aux, 0, n - 1);
4 delete[] aux;
5}
1void r_mergesort(int *A, int *aux, int lo,int hi) {
2
3 //basecase(single element or empty list)
4 if (hi <= lo) return;
5
6 //divide
7 int mid = lo + (hi - lo) / 2;
8
9 //recursively sort halves
10 r_mergesort(A, aux, lo, mid);
11 r_mergesort(A, aux, mid + 1, hi);
12
13 //merge results
14 merge(A, aux, lo, mid, hi);
15}
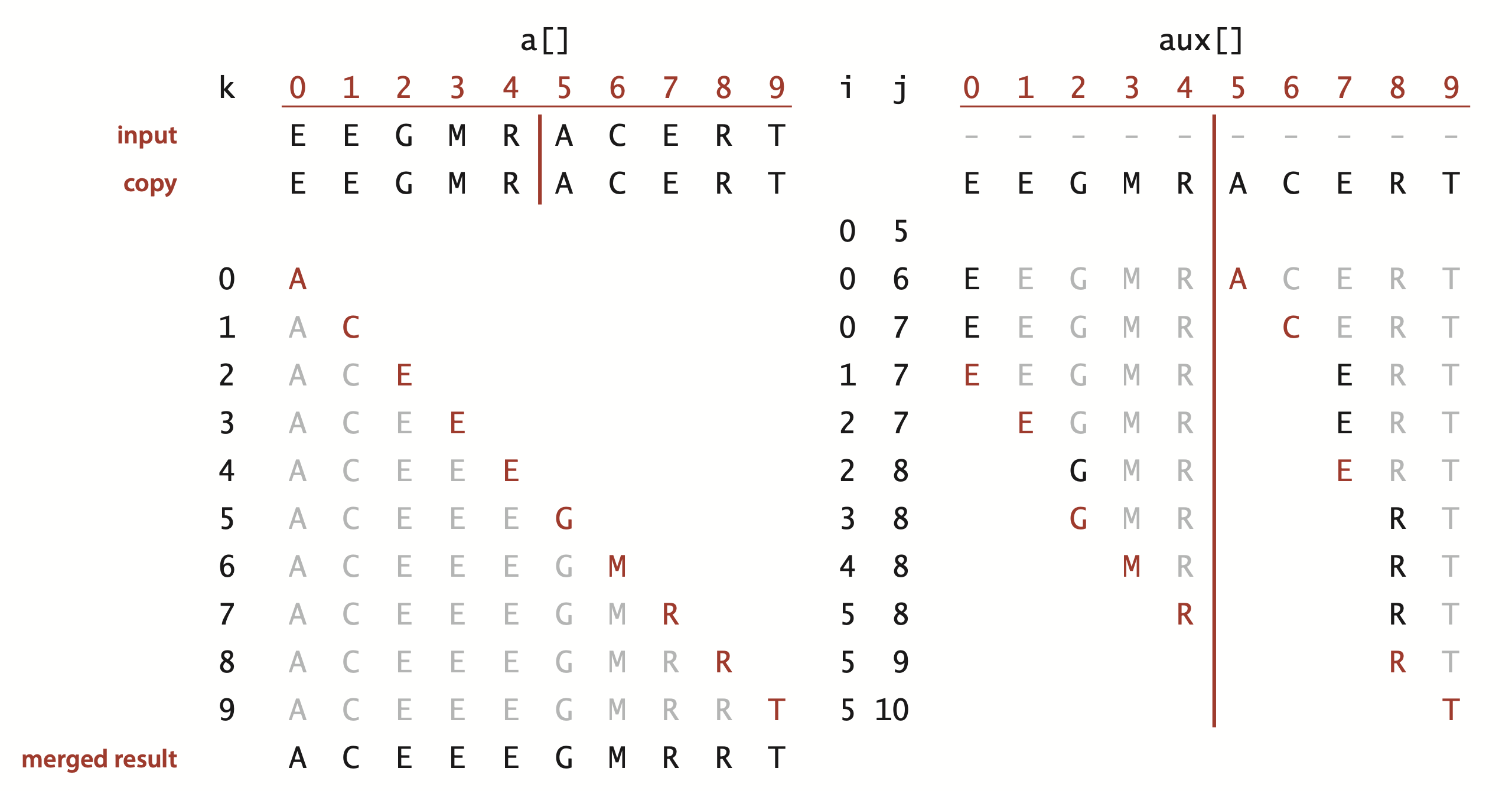
1void merge (int *A, int *aux, int lo, int mid,int hi) {
2
3 // copy array
4 std::memcpy(aux + lo, A + lo, (hi - lo + 1 * sizeof(A)));
5
6 // merge
7 int i = lo, j = mid + 1;
8
9 for (int k = lo; k <= hi; k++) {
10
11 if (i > mid) A[k]=aux[j++];
12
13 else if (j > hi) A[k] = aux[i++];
14
15 else if(aux[j] < aux[i]) A[k] = aux[j++];
16
17 else A[k] = aux[i++];
18 }
19}
Divide & Conquer#
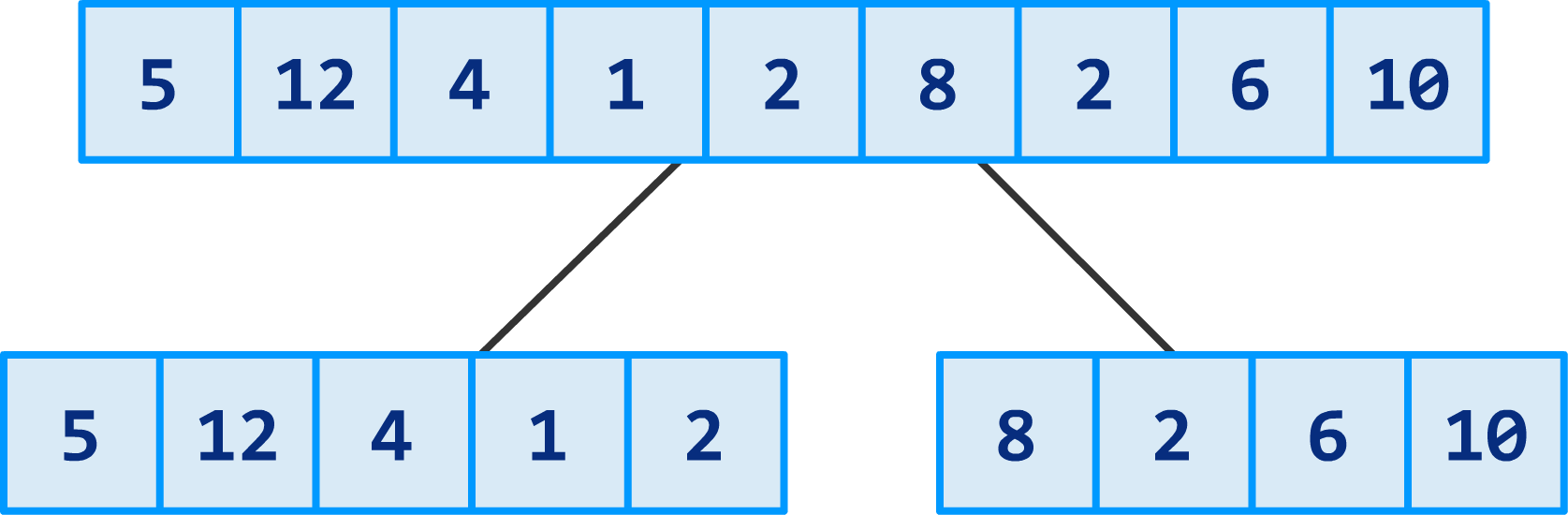
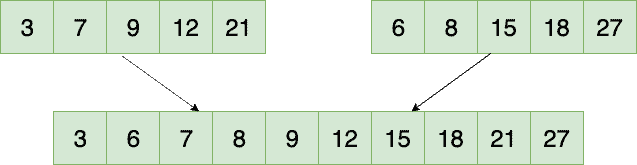
Merging two sorted arrays#
Analysis (recurrence)#
Worst Case |
Average Case |
Best Case |
|
|---|---|---|---|
Time Complexity |
\(\Theta(n\ log\ n)\) |
\(\Theta(n\ log\ n)\) |
\(\Theta(n\ log\ n)\) |
A merge sort consists of several passes over the input.
\(1^{st}\) Pass: merges segments of size 1
\(2^{nd}\) Pass: merges segments of size 2
\(i^{th}\) Pass: merges segments of size \(2^{i-1}\).
Total number of passes: \(log\ n\)
As merge showed, we can merge two sorted segments in linear time, which means that each pass takes \(O(n)\) time. Since there are \(log\ n\) passes, the total computing time is \(\Theta(n\ log\ n)\), or expressed as:
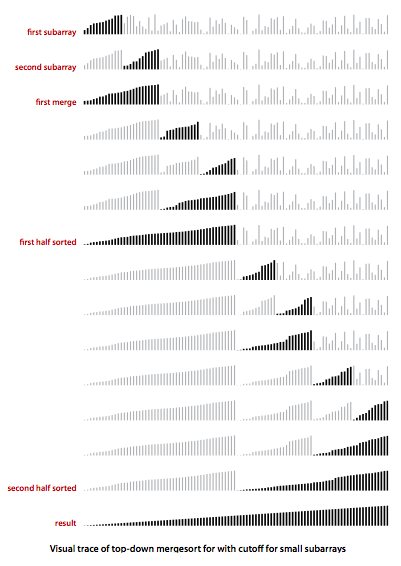
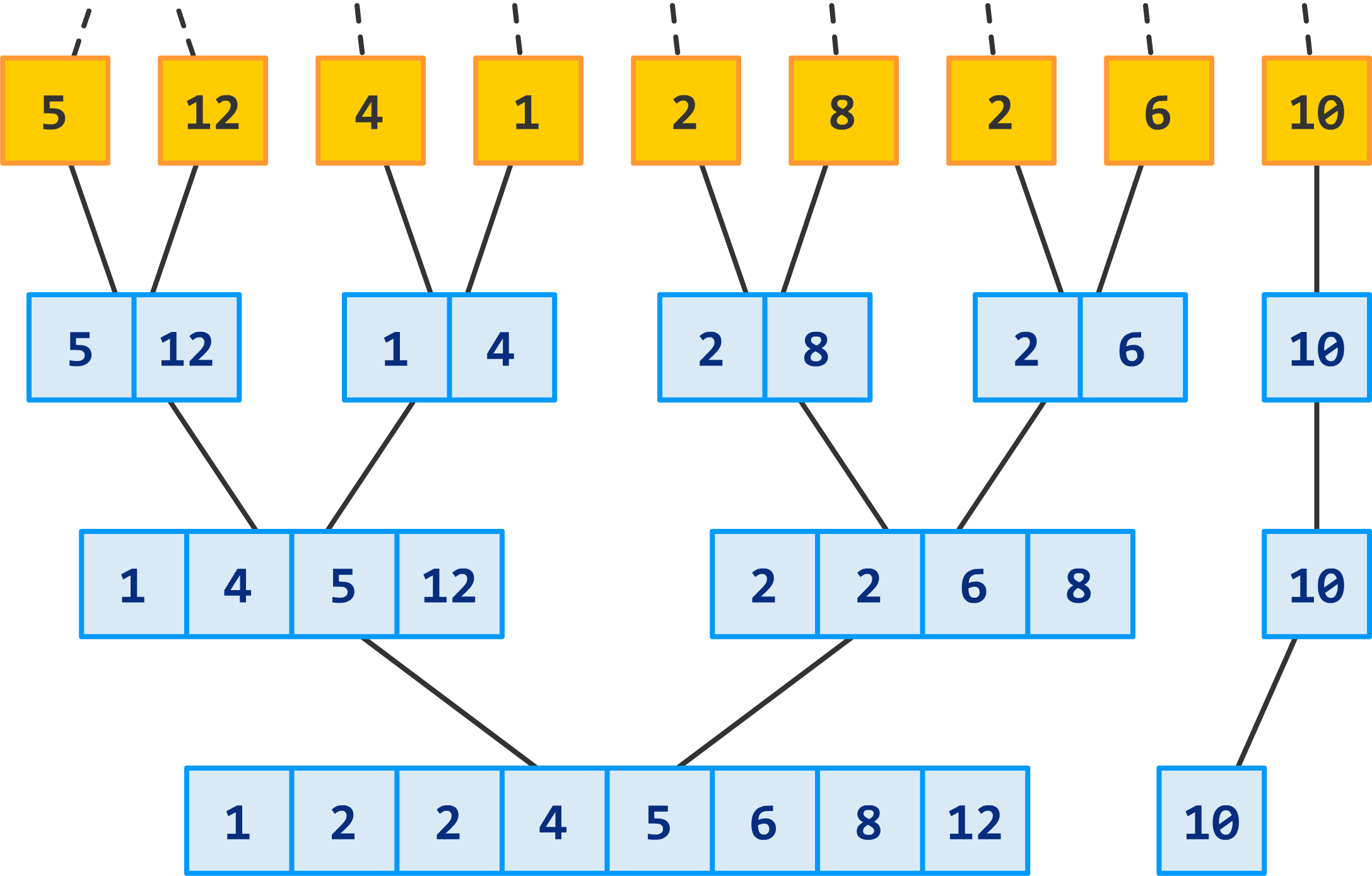
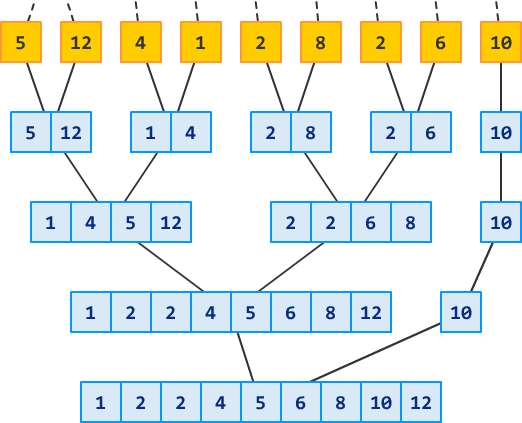
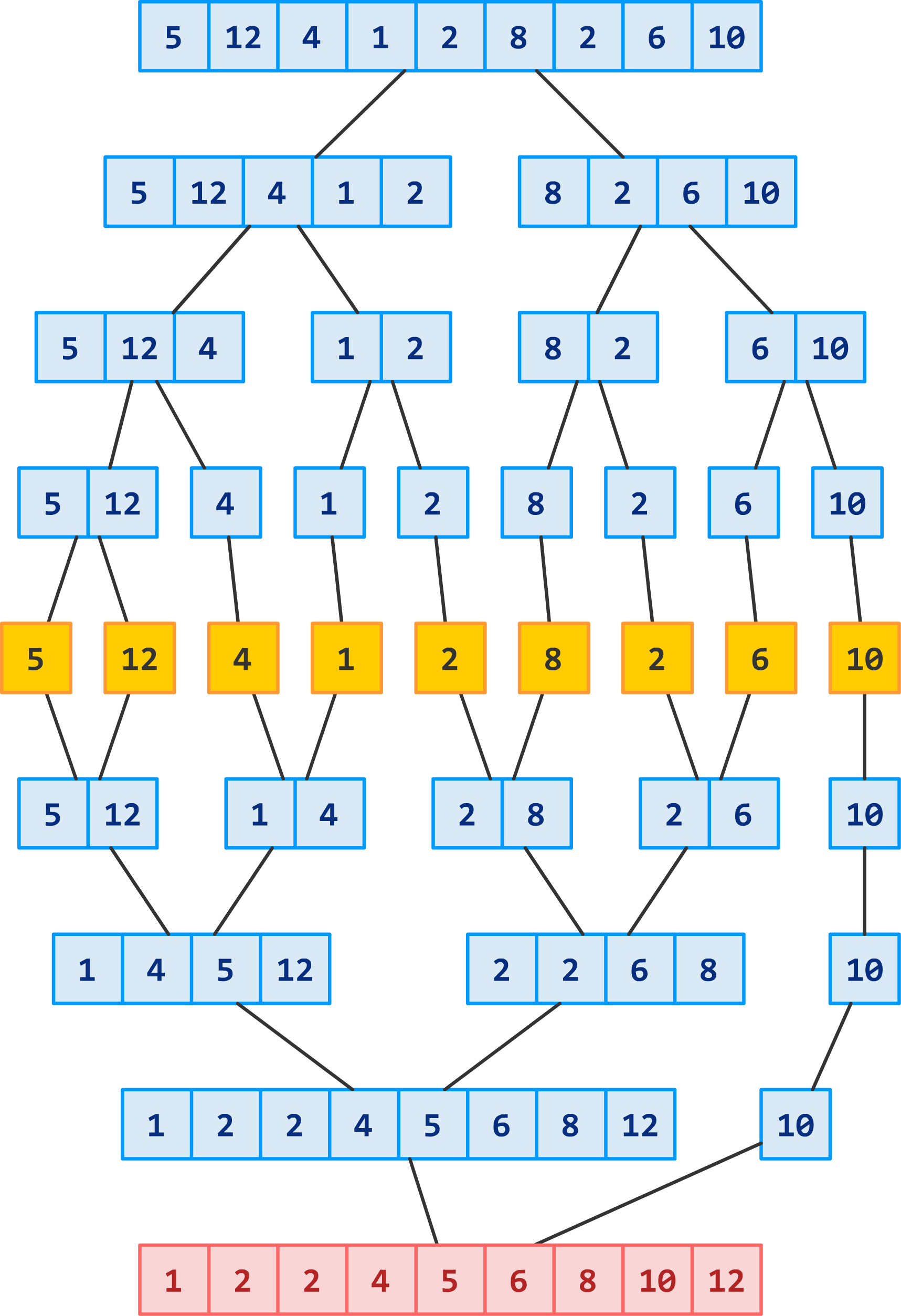
Recursion Tree (trace)#
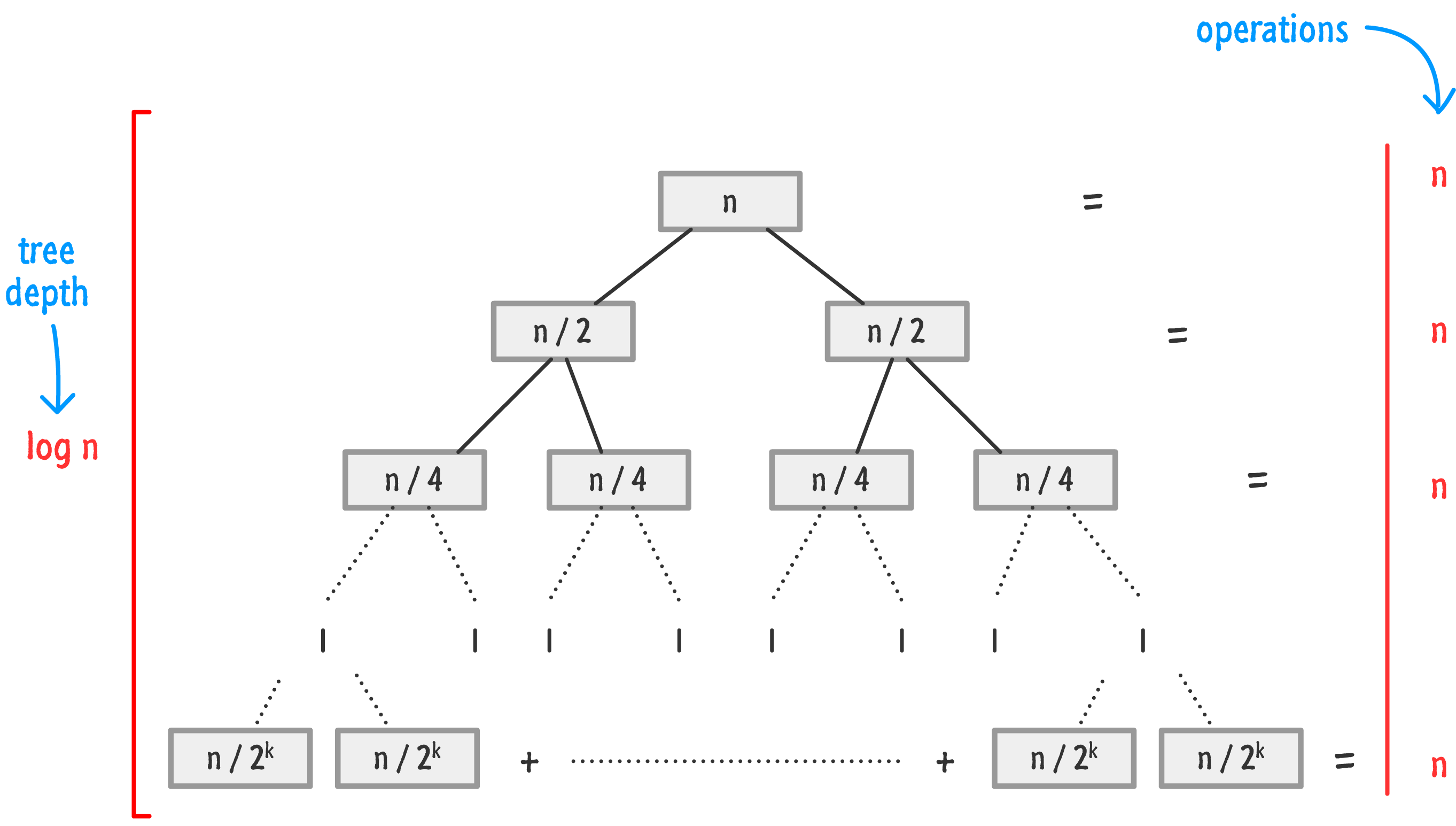
Try It!
Total time for \(mergeSort\) is: the sum of the merging times for all the levels
If there are \(l\) levels in the tree, then the total merging time is \(l * cn\)
Where \(l\) is the number of subproblem levels until subproblems reach size \(n\)
For total time, we end up with:
Discard the low-order term (constant) and the coefficient
Sorting Visualizer#
Example#
solution 1
Use an additional array of equal size
what is the required extra memory?
solution 2
Exchange first and last and work recursively on the inner part
can do it iteratively as well
what is the required extra memory?
In-place sorting#
An algorithm does not use extra space for manipulating the input but may require a small though non-constant extra space for its operation. Usually, this space is \(O(log\ n)\), though sometimes anything in \(O(n)\) (Smaller than linear) is allowed.
1void selectionSort(int arr[], int n)
2{
3 int i, j, min_idx;
4
5 // One by one move boundary of unsorted subarray
6 for (i = 0; i < n-1; i++) {
7
8 // Find the minimum element in unsorted
9 // array
10 min_idx = i;
11 for (j = i+1; j < n; j++)
12
13 if (arr[j] < arr[min_idx]) min_idx = j;
14
15 // Swap the found minimum element with
16 // the first element
17 if(min_idx!=i)
18 swap(&arr[min_idx], &arr[i]);
19 }
20}
In-place?
Yes, it does not require extra space.
1void insertionSort(int arr[], int n)
2{
3 int i, key, j;
4
5 for (i = 1; i < n; i++)
6 {
7 key = arr[i];
8 j = i - 1;
9
10 // Move elements of arr[0..i-1],
11 // greater than key, to one position
12 // ahead of their current position
13 while (j >= 0 && arr[j] > key)
14 {
15 arr[j + 1] = arr[j];
16 j = j - 1;
17 }
18 arr[j + 1] = key;
19 }
20}
In-place?
Yes, it does not require extra space.
Stable Sorting#
Stability
A sorting algorithm is stable if it preserves the order of equal elements
Consider sorting (in ascending order) a list \(A\) into a sorted list \(B\). Let \(f(i)\) be the index of element \(A[i]\) in \(B\). The sorting algorithm is stable if:
for any pair \((i,j)\) such that \(A[i] = A[j]\) and \(i < j\), then \(f(i) < f(j)\)
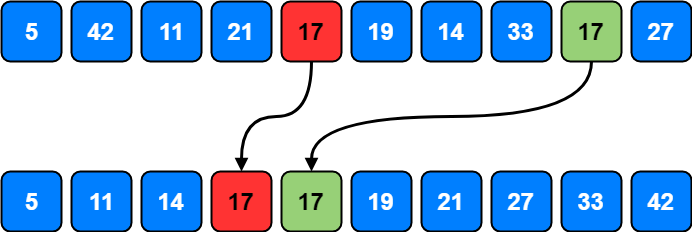
Stability#
Is selection sort stable?
Selection sort algorithm picks the minimum and swaps it with the element at current position.
Suppose the array is:
After iteration 1:
2 will be swapped with the element in 1st position:
So our array becomes:
Since now our array is in sorted order and we clearly see that \(5_a\) comes before \(5_b\) in initial array but not in the sorted array.
Therefore, selection sort is not stable.
NOT STABLE
long distance swaps
try: 5 2 3 8 4 5 6
Is insertion sort stable?
STABLE
equal items never pass each other (depends on correct implementation)
Sorting Algorithms#
Best-Case |
Average-Case |
Worst-Case |
Stable |
In-place |
|
|---|---|---|---|---|---|
Selection Sort |
|||||
Insertion Sort |
|||||
Merge Sort |
Best-Case |
Average-Case |
Worst-Case |
Stable |
In-place |
|
|---|---|---|---|---|---|
Selection Sort |
\(\Theta(n^2)\) |
\(\Theta(n^2)\) |
\(\Theta(n^2)\) |
No |
Yes |
Insertion Sort |
\(\Theta(n)\) |
\(\Theta(n^2)\) |
\(\Theta(n^2)\) |
Yes |
Yes |
Merge Sort |
\(\Theta(n\ log\ n)\) |
\(\Theta(n\ log\ n)\) |
\(\Theta(n\ log\ n)\) |
Yes |
No |
Test Yourself…#
Mergesort Merging Proficiency Exercise
Mergesort Proficiency Exercise




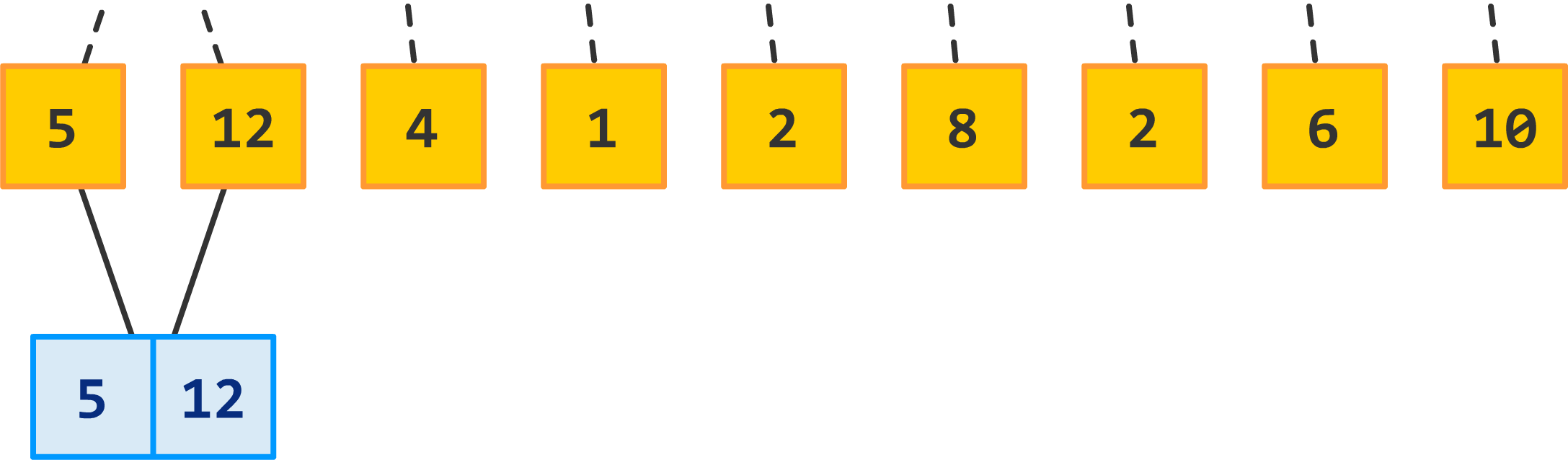
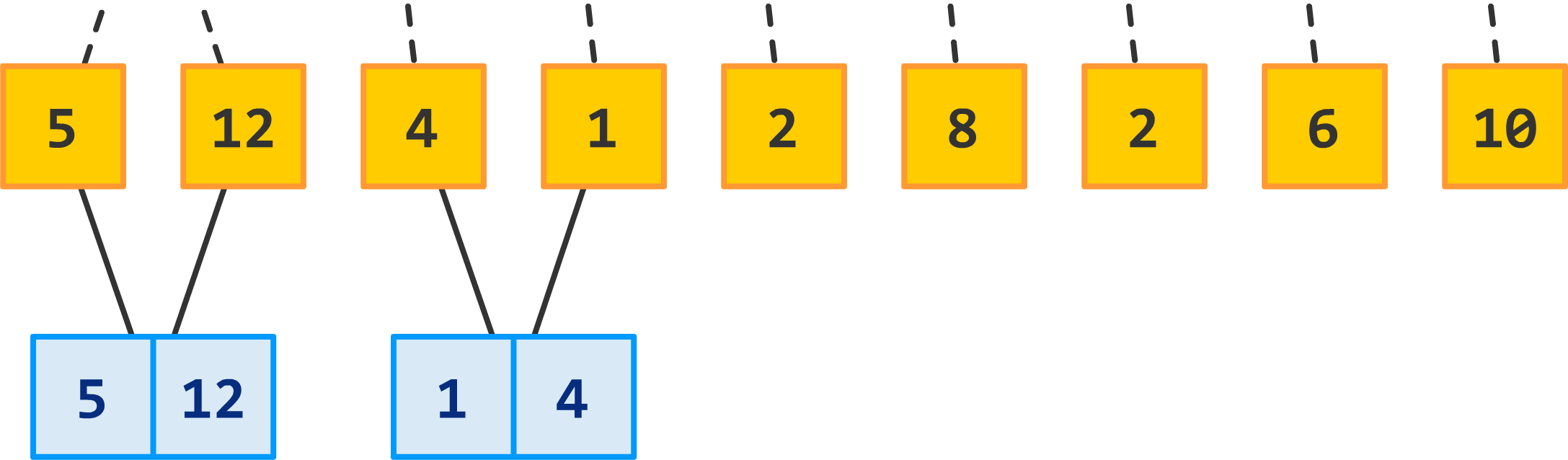
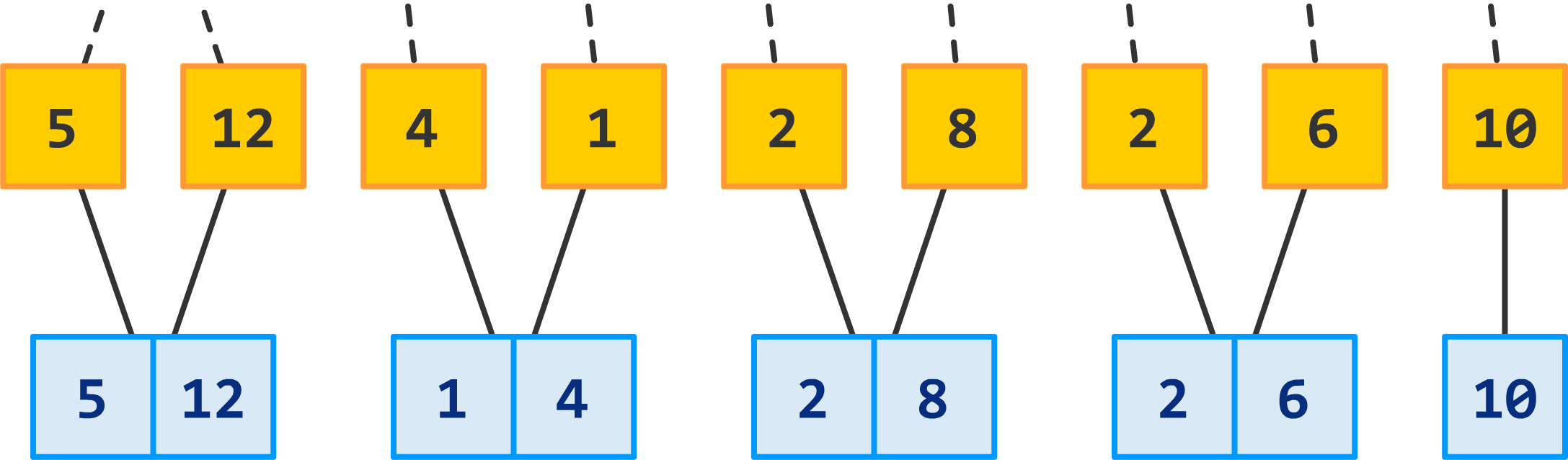
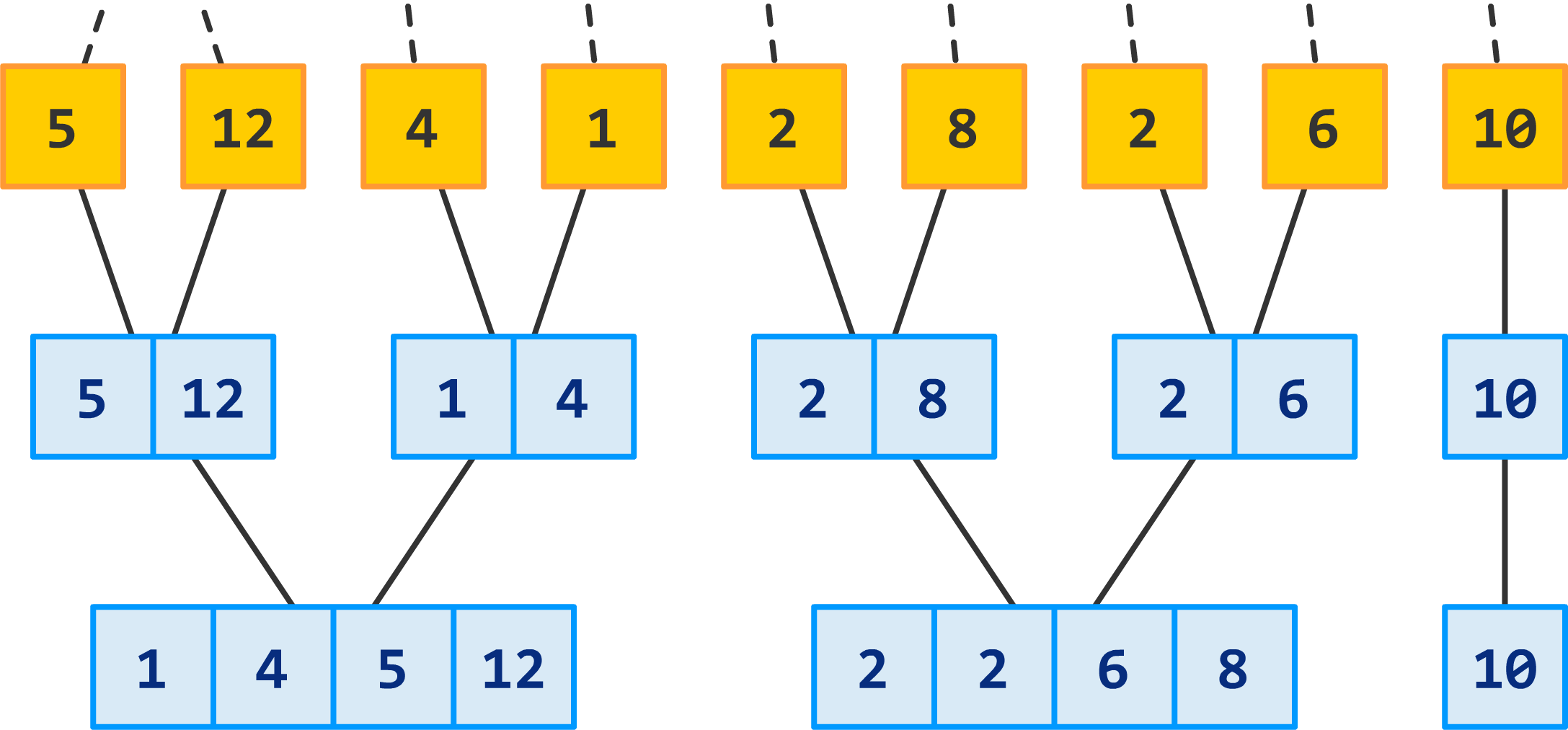

Comments on Merge Sort#
Advantages
relatively efficient for sorting large datasets
stable sort : the order of elements with equal values is preserved during the sort
easy to implement
useful for external sorting
requires relatively few additional resources (such as memory)
Disadvantages
slower compared to the other sort algorithms for smaller tasks
requires an additional memory space of 0(n) for the temporary array
regardless of sort status, goes through whole process
requires more code to implement