Analysis#
Overview#
- Algorithm analysis#
the process of evaluating the performance of an algorithm in terms of time and space complexity. This is essential for determining the efficiency of algorithms and data structures and is used to identify the best algorithm for a particular problem.
- Computational cost#
the resources required to execute an algorithm. These resources can include time, space, and hardware requirements, among others. The computational cost of an algorithm is generally expressed in terms of its time complexity and space complexity.
- Time complexity#
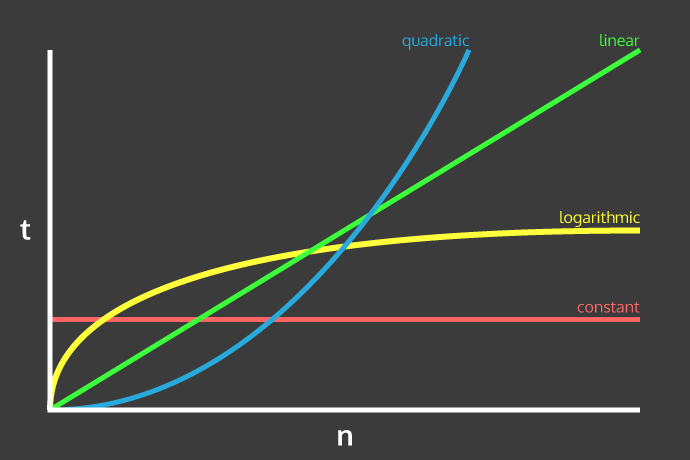
the amount of time required by an algorithm to complete its execution. It is usually expressed in terms of the number of operations performed by the algorithm as a function of the input size. Common time complexities include
\[O(1), O(log\ n), O(n), O(n\ log\ n), O(n^2), O(2^n)\]- Space complexity#
the amount of memory required by an algorithm to execute. It is usually expressed in terms of the amount of memory required by the algorithm as a function of the input size. Common space complexities include
\[O(1), O(log\ n), O(n), O(n\ log\ n), O(n^2), O(2^n)\]- Asymptotic analysis#
a method used to analyze the time and space complexity of an algorithm as the input size approaches infinity. It is a way of characterizing the growth rate of an algorithm and is usually expressed in terms of big O notation. Big O notation provides an upper bound on the growth rate of an algorithm and is commonly used to compare the efficiency of different algorithms. For example, an algorithm with a time complexity of \(O(n)\) is said to be less efficient than an algorithm with a time complexity of \(O(log\ n)\) as the input size approaches infinity.
The choice of data structure can also have a significant impact on the computational cost of an algorithm. Different data structures have different time and space complexity characteristics, and the choice of data structure can greatly affect the efficiency of an algorithm. For example, using a binary search tree instead of an array for searching can greatly reduce the time complexity of the algorithm.
Overall, understanding algorithm analysis, computational cost, and asymptotic analysis is essential for computer scientists and programmers, as it is crucial for developing efficient algorithms and data structures.