Heaps

TL;DR

A heap is a specialized tree-based data structure in computer science that is used to maintain a collection of elements with a specific ordering property. A heap is usually implemented as a binary tree, where each node has at most two children, and it satisfies the heap property.

The heap property ensures that the root node has either the minimum or maximum value among all the nodes in the heap, depending on whether it is a min-heap or max-heap. In a min-heap, the value of each node is greater than or equal to the value of its parent, while in a max-heap, the value of each node is less than or equal to the value of its parent.

Heaps are commonly used in algorithms that require efficient access to the maximum or minimum element in a collection, such as heap sort, priority queues, and graph algorithms like Dijkstra’s algorithm for finding shortest paths. The advantage of using a heap data structure is that it allows these algorithms to access the minimum or maximum element in constant time, making them highly efficient.

In addition to binary heaps, there are other types of heaps, such as Fibonacci heaps, binomial heaps, and pairing heaps, each with its own advantages and disadvantages.

Additional Resources

• Data Structures: Heaps | HackerRank

• Heaps in 6 minutes — Methods | Michael Sambol

• Heap sort in 4 minutes | Michael Sambol

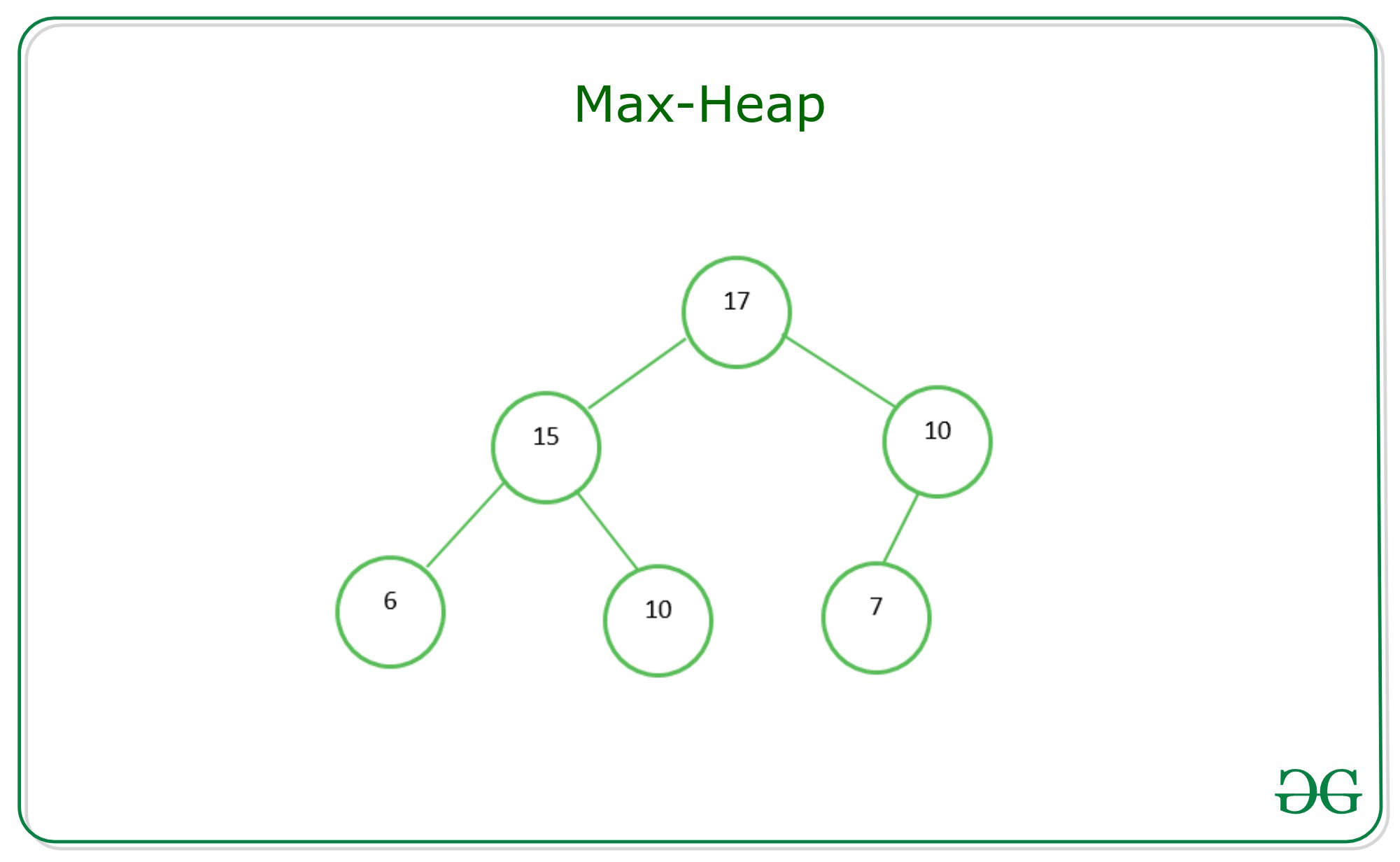
(max) Heap

Structure Property

a heap is a complete binary tree

Heap-Order Property

for every node \(x\):

• \(key\ parent\ x\ \ge\ key \ x\)

• except the root, which has no parent

Height of a heap

What is the minimum number of nodes in a complete binary tree of height \(h\)?

\[n \ge 2^h\Rightarrow\ log\ n \ge log\ 2^h \Rightarrow\ log\ n \ge h\]

Implementation

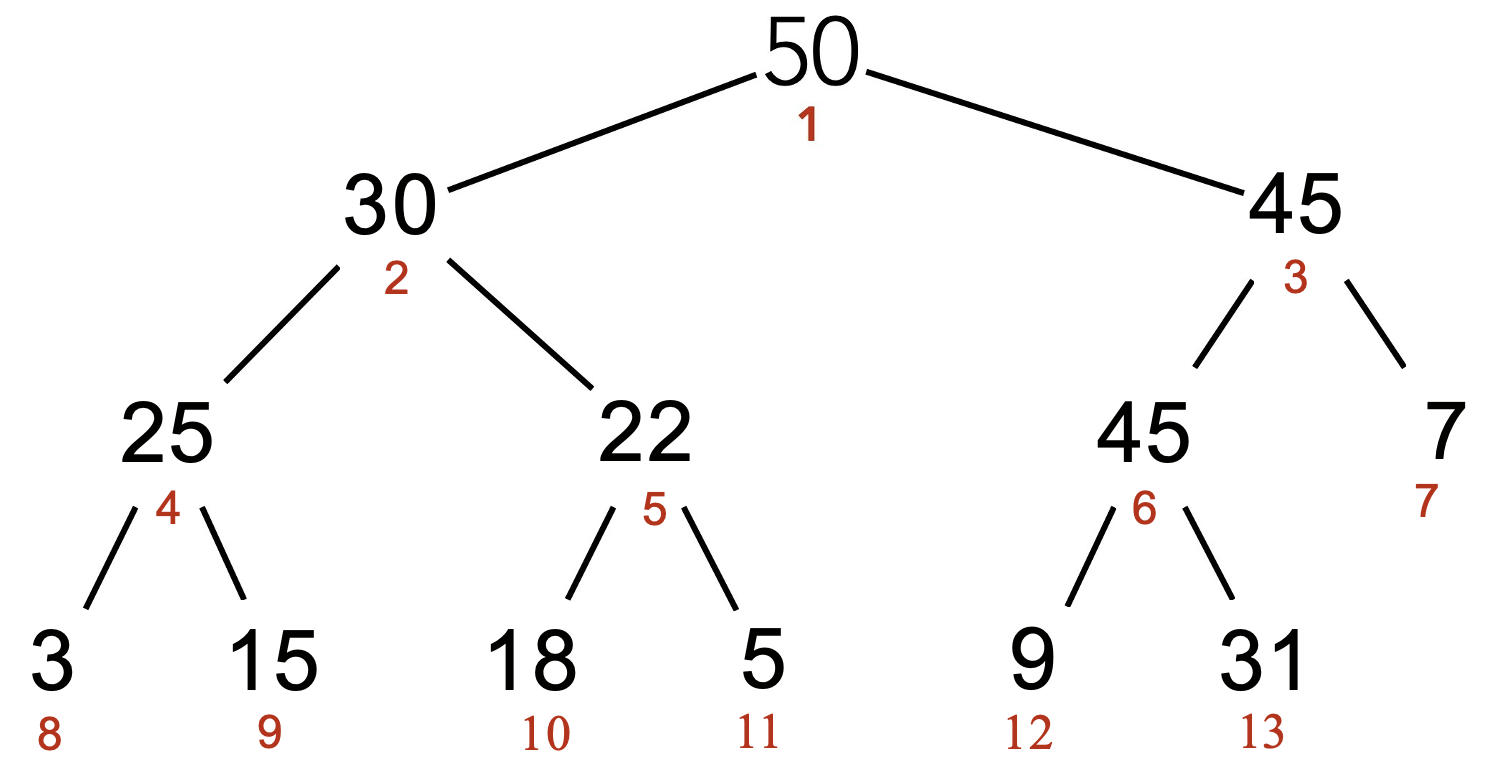
node(i)

\[i\]

parent(i)

\[floor(\frac{i}{2})\]

left_child(i)

\[i * 2\]

right_child(i)

\[i * 2 + 1\]

\(insert\)

Append new element to the end of array

Check heap-order property

if violated, Up-Heap (swap with parent)

repeat until heap-order is restored

if not, \(insert\) complete

Time Complexity

\(O(log\ n)\)

\(removeMax\)

Max element is the first element of the array

the \(root\) of the heap

Copy last element of array to the first position

then decrement array size by 1 (removes the last element)

Check heap-order property

if violated, Down-Heap (swap with larger child)

repeat until heap-order is restored

if not, insert complete

Time Complexity

\(O(log\ n)\)

Performance

	Sorted Array/List	Unsorted Array/List	Heap
insert	\(O(n)\)	\(O(1)\)	\(O(log\ n)\)
removeMax	\(O(1)\)	\(O(n)\)	\(O(log\ n)\)
max	\(O(1)\)	\(O(n)\)	\(O(1)\)
insert N	\(O(n^2)\)	\(O(n)\)	\(O(n)^{**}\)

(**) assuming we know the sequence in advance (buildHeap)