Graphs : Depth-First Search

TL;DR

Depth-first search (DFS) is a graph traversal algorithm that visits all the vertices in a graph by exploring as far as possible along each branch before backtracking. DFS starts at a specified vertex (the starting vertex) and then follows one of its edges to an adjacent vertex. It then recursively applies the same process to the adjacent vertex, and continues until it reaches a dead end (i.e., a vertex with no unvisited adjacent vertices). It then backtracks to the most recently visited vertex with unvisited adjacent vertices, and repeats the process until all vertices have been visited.

DFS can be used to perform a variety of operations on a graph, such as finding a path between two vertices, checking whether the graph is connected, and identifying cycles in the graph. DFS can also be modified to search for solutions in a problem space, such as finding the shortest path between two points in a maze.

DFS can be implemented using either a recursive or iterative approach. The recursive approach uses a function call stack to keep track of the visited vertices and backtrack when necessary. The iterative approach uses a stack data structure to keep track of the visited vertices and their adjacent vertices.

Overall, DFS is an important algorithm in graph theory and is widely used in many applications, such as network analysis, data mining, and artificial intelligence.

Additional Resources

DFS

Reachability

Problem

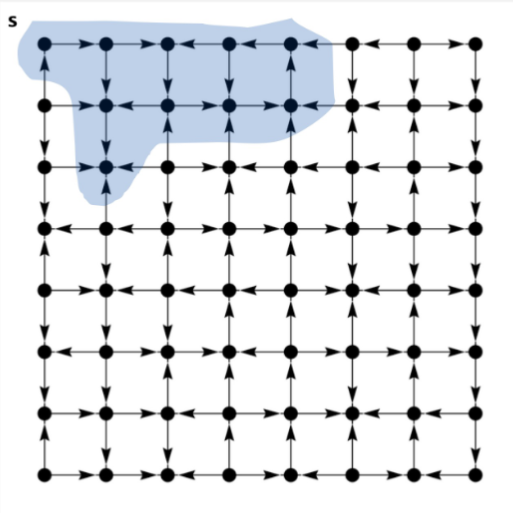
Given a digraph \(G\) and vertex \(s\), find all the vertices reachable from \(s\)

DFS

Goal

Systemically traverse a digraph

void Graph::dfs( Vertex v )
{
  v.visited = true;
  for each Vertex w adjacent to v
    if( !w.visited )
      dfs( w );
}

Typical applications

Reachability: finding all vertices reachable from a given vertex
Path finding: find directed path from one vertex to another

Directed-DFS

To visit vertex \(v\):

Mark vertex \(v\)
Recursively visit all unmarked vertices adjacent from \(v\)

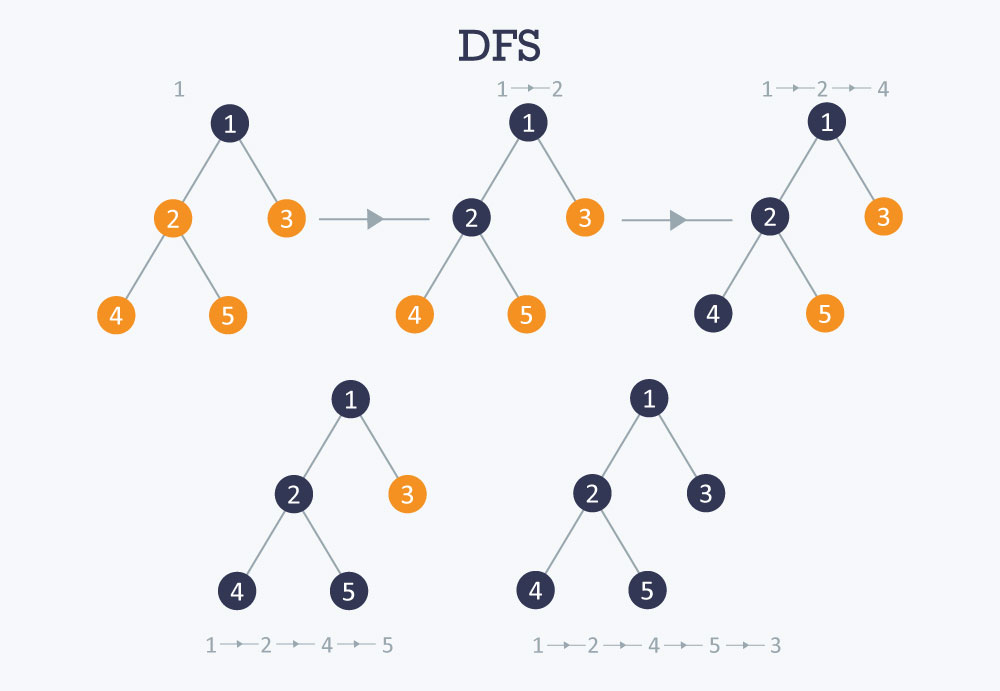
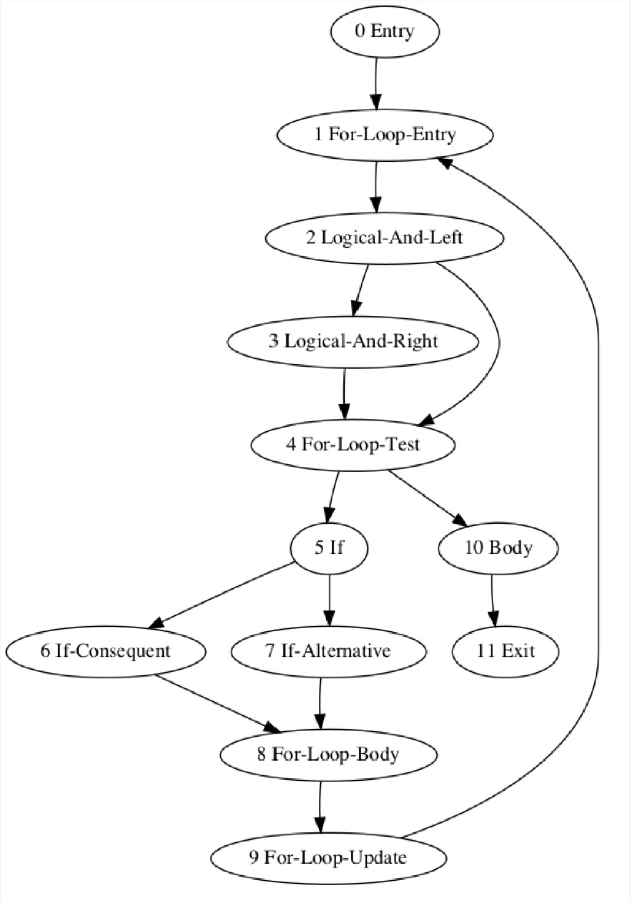
Fig. 75 directed dfs

Properties

Proposition

DFS marks all vertices reachable from \(s\) in \(\Theta(E+V)\) time in the worst case

Proof

Initializing an array of length \(v\) takes \(\Theta(V)\) time
Each vertex is visited at most once
Visiting a vertex takes time proportional to its outdegree:

\[outdegree(v_0) + outdegree(v_1) + outdegree(v_2) + \dots = E\]

\[in\ worst\ case,\ all\ V\ vertices\ reachable\ from\ s\]

Note

If all vertices are reachable from \(s\), then \(E \ge V - 1\), so \(V\) is a lower-order term

Application 1

Program control-flow analysis

Every program is a digraph

Vertex = basic block of instructions (straight-line program)
Edge = jump

Dead-code elimination

Find (and remove) unreachable code

Infinite-loop detection

Determine whether exit is unreachable

Application 2

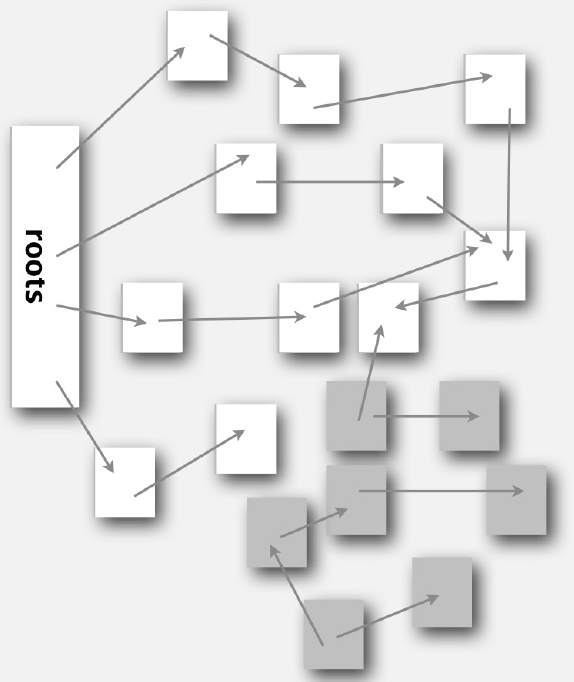
Mark-sweep garbage collection

Every program is a digraph

Vertex = basic block of instructions (straight-line program) Edge = jump

Roots

Objects known to be directly accessible by a program (eg stack frame)

Reachable objects

Objects indirectly accessible by program (starting at a root and following a chain of pointers)

Memory cost

Uses 1 extra mark bit per object (plus DFS function-call stack)

Path Finding

Directed Path DFS

Goal

DFS determines which vertices are reachable from s. How to reconstruct paths?

Solution

Use parent-link representation

Fig. 76 reachable from \(0\)

Fig. 77 parent-link representation of paths from vertex \(0\)

Parent-link

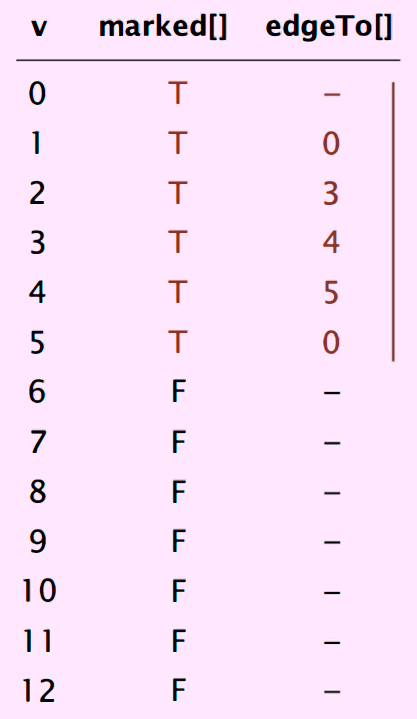
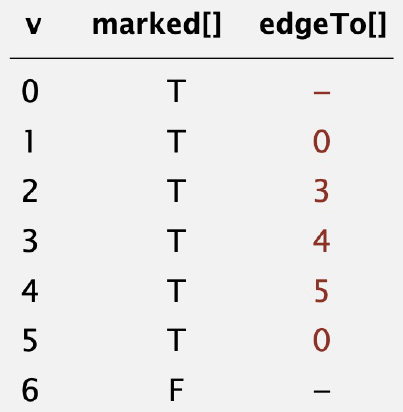
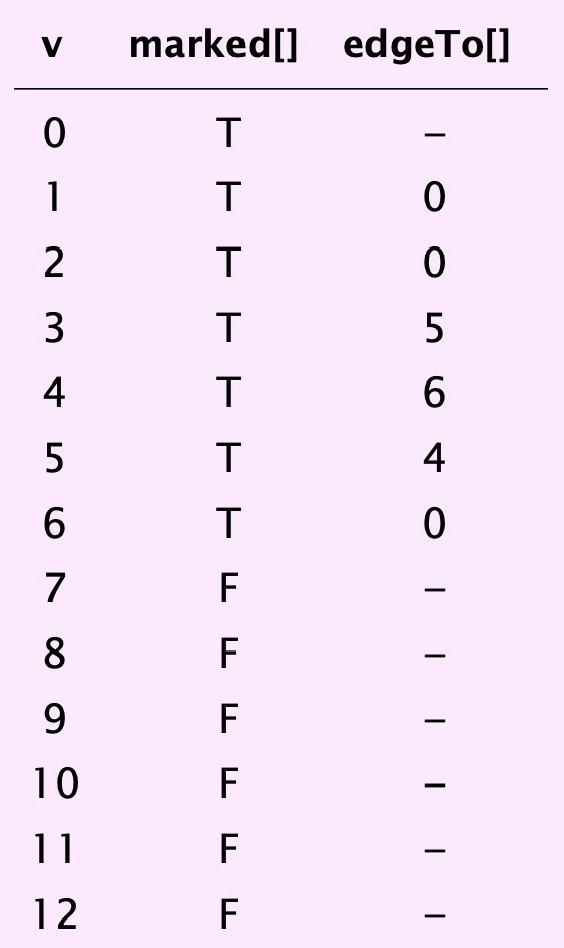
Parent-link representation of paths from \(s\)

Maintain an integer array \(edgeTo[]\)
Interpretation: \(edgeTo[v]\) is the next-to-last vertex on a path from \(s\) to \(v\)
To reconstruct path from \(s\) to \(v\), trace \(edgeTo[]\) backward from \(s\) to \(v\) (and reverse)

Fig. 78 reachable from \(0\)

Fig. 79 parent-link representation of paths from vertex \(0\)

public Iterable<Integer> pathTo(int v) {
  if (!marked[v]) return null; 
  Stack<Integer> path = new Stack<>(); 
  for (int x = v; x != s; x = edgeTo[x]) 
    path.push(x); 
  path.push(s); 
  return path; 
}

Undirected Graphs

Flood Fill

Problem

Implement flood fill (Photoshop magic wand)

Fig. 80 magic wand tool

Graphs

Problem

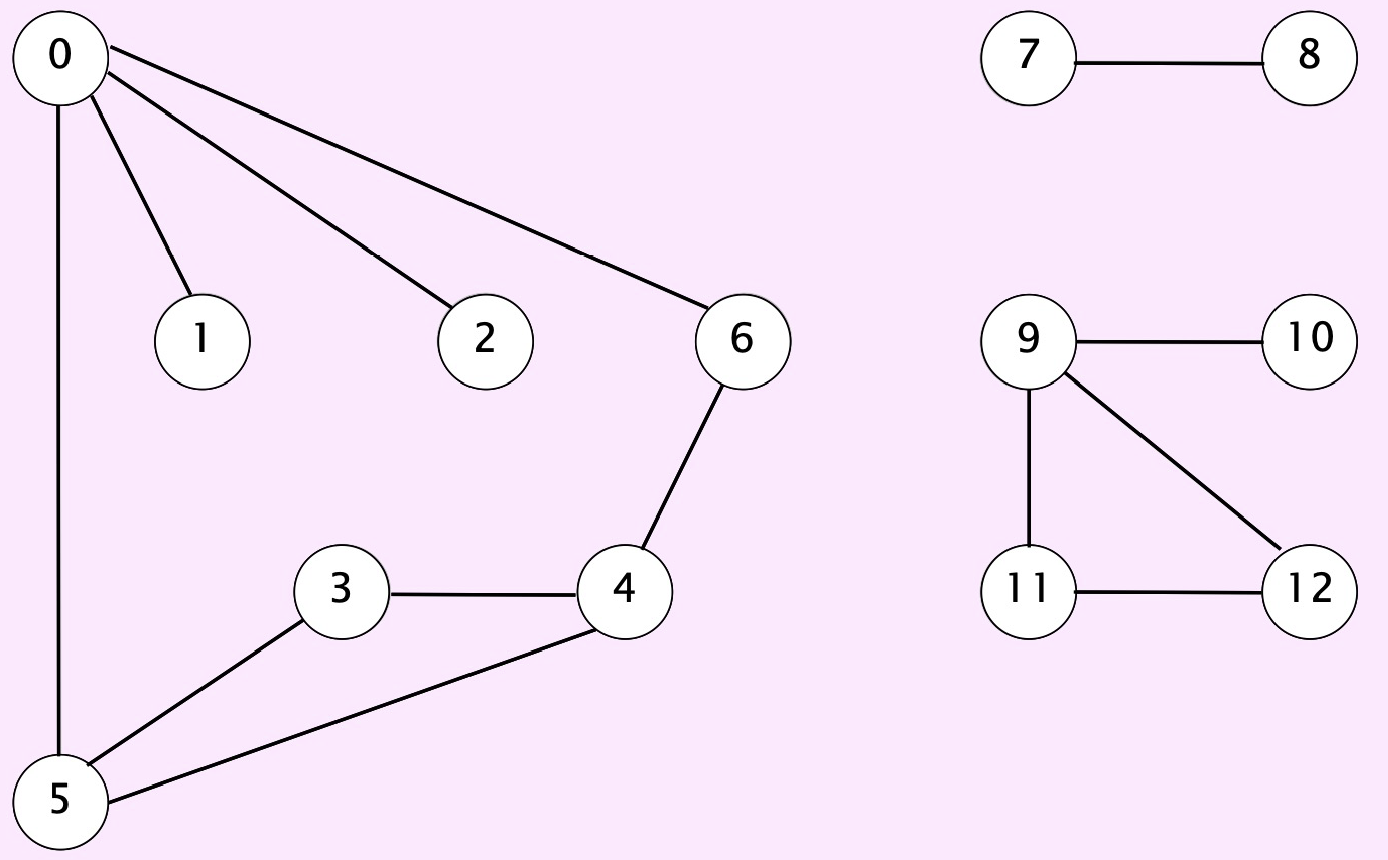
Given an undirected graph \(G\) and vertex \(s\), find all vertices connected to \(s\)

Solution

Treat undirected graph as a digraph, replacing each edge with two antiparallel edges

DFS (to visit a vertex v)
------------------------
Mark vertex v.
Recursively visit all unmarked
    vertices w adjacent to v

Typical applications

Find all vertices connected to a given vertex Find a path between two vertices

Undirected Search

To visit vertex \(v\):

Mark vertex \(v\)
Recursively visit all unmarked vertices adjacent from \(v\)

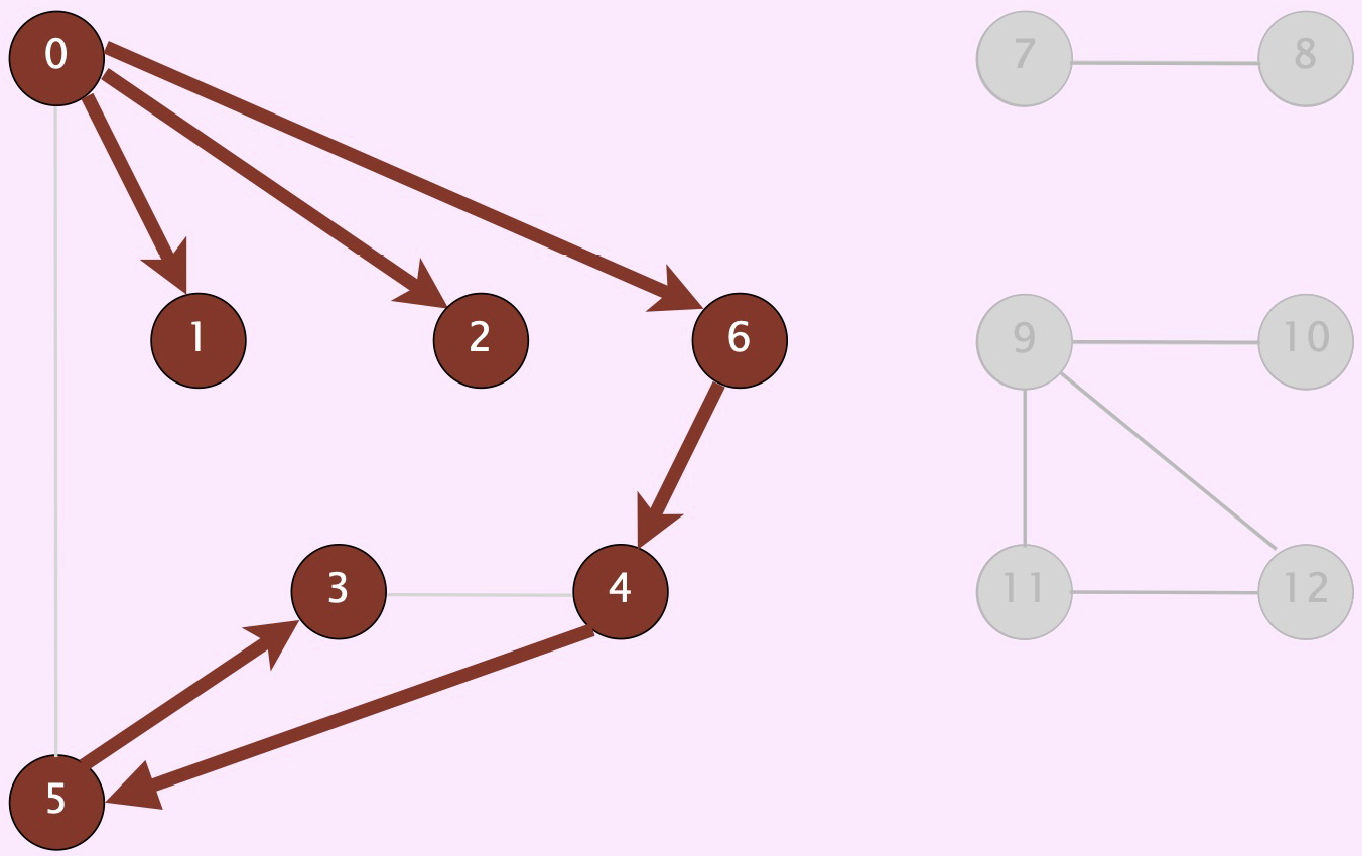
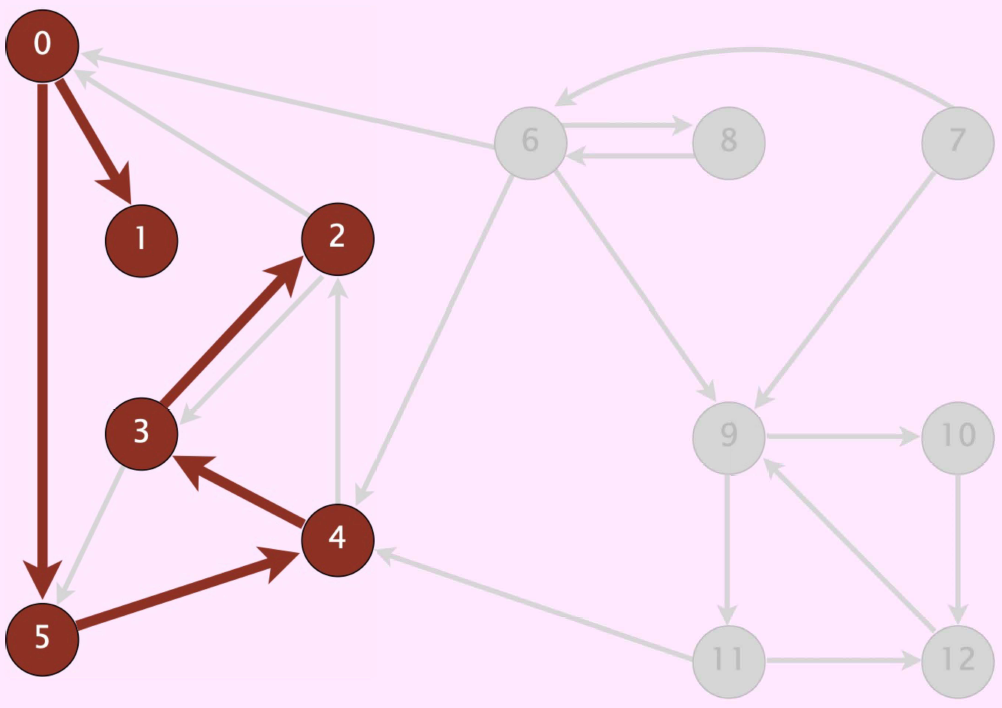
Fig. 81 vertices connected to \(0\) (and associated paths)

Search

Tree traversal

Many ways in a binary tree

stack/recursion

\[\begin{split}\begin{align} Inorder & \ \ \ \ \ \{ A, C, E, H, M, R, S, X \} \\ Preorder & \ \ \ \ \ \{ S, E, A, C, R, H, M, X \}\\ Postorder & \ \ \ \ \ \{ C, A, M, H, R, E, X, S \} \\ \end{align}\end{split}\]

queue

\[Level-order \ \ \ \ \ \{ S, E, X, A, R, C, H, M \} \]

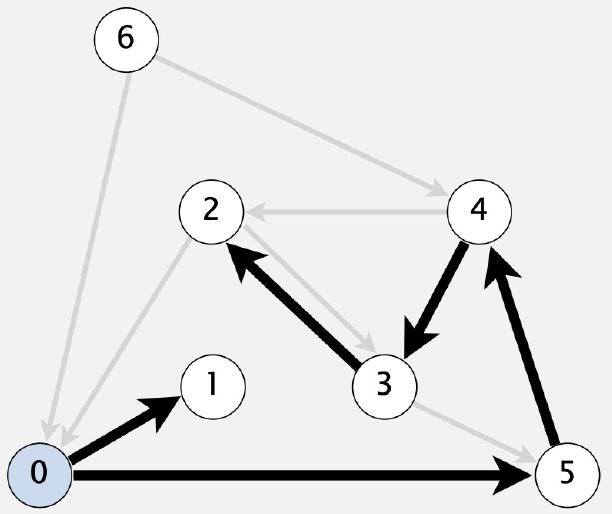
Fig. 82 parent-link representation of paths from vertex \(0\)

Graph search

Many ways to explore a graph

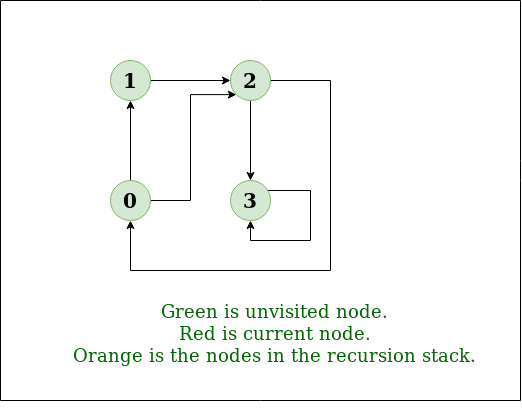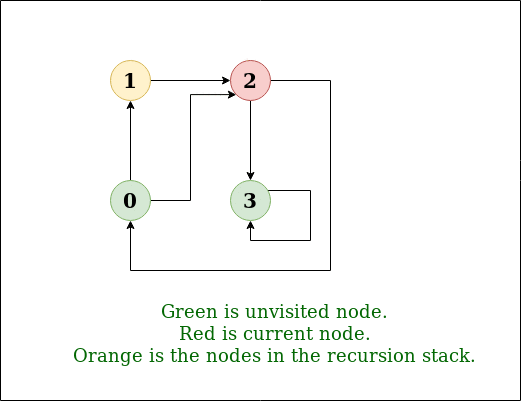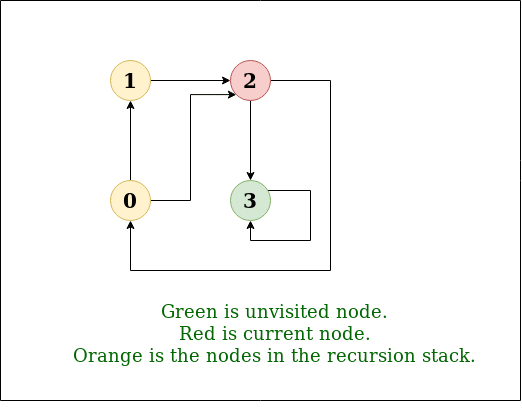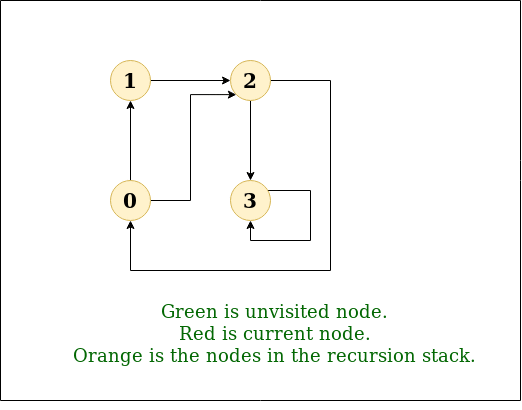
• DFS preorder: vertices in order of calls to \(dfs(G,v)\)

• DFS postorder: vertices in order of return calls from \(dfs(G,v)\)

• Breadth-first: vertices in increasing order of distance from \(s\)